
分析 (1)由二次函数的顶点坐标可知对称轴为直线x=-1,再根据图象过坐标原点,利用二次函数的对称性即可求出点A的坐标;
(2)由二次函数的图象过原点O,可设此解析式为y=ax2+bx,把B(-1,-1)代入,得出a-b=-1.利用根与系数的关系得出A点横坐标为-$\frac{b}{a}$,再根据OA=3,得出|-$\frac{b}{a}$|=3,那么$\frac{b}{a}$=±3,即b=3a,或b=-3a.分别代入a-b=-1,利用二次函数的性质即可求解.
解答 解:(1)∵点B(-1,-1)为该二次函数的图象的顶点,
∴该二次函数的对称轴为直线x=-1,
∵二次函数的图象与x轴有两个交点O、A,其中点O为坐标原点,
∴点A的坐标是(-2,0);
(2)∵二次函数的图象过原点O,
∴可设此解析式为y=ax2+bx,
∵该函数图象经过点B(-1,-1),
∴a-b=-1.
∵二次函数的图象与x轴有两个交点O、A,
∴A点横坐标为-$\frac{b}{a}$,
∵OA=3,
∴|-$\frac{b}{a}$|=3,
∴$\frac{b}{a}$=±3,
∴b=3a,或b=-3a.
当b=3a时,代入a-b=-1,得a=$\frac{1}{2}$,b=$\frac{3}{2}$,抛物线为y=$\frac{1}{2}$x2+$\frac{3}{2}$x,开口向上,二次函数没有最大值;
当b=-3a时,代入a-b=-1,得a=-$\frac{1}{4}$,b=$\frac{3}{4}$,抛物线为y=-$\frac{1}{4}$x2+$\frac{3}{4}$x,开口向下,二次函数有最大值,最大值为$\frac{9}{16}$.
综上所述,若OA=3,该二次函数的最大值为$\frac{9}{16}$.
点评 本题考查了抛物线与x轴的交点,二次函数的性质,二次函数图象上点的坐标特征以及二次函数最值的求法,都是基础知识,需熟练掌握.本题难度适中.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:解答题
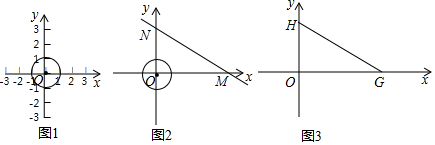
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
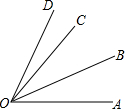 如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )
如图所示,OB是∠AOC平分线,∠COD=$\frac{1}{3}$∠BOD,∠COD=17°,则∠AOD的度数是( )| A. | 70° | B. | 83° | C. | 68° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
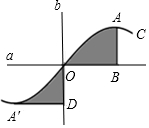 如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为6.
如图,直线a、b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是点A',AB⊥a于点B,A'D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
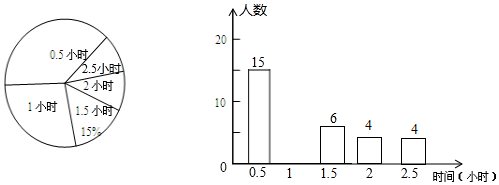
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com