
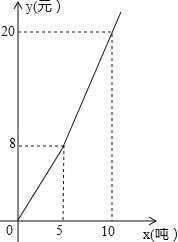
【题目】随着地球上的水资源日益枯竭,各级政府越来越重视节约用水.某市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中 x 表示人均月生活用水的吨数,y 表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:
(1)该市人均月生活用水的收费标准是:不超过 5 吨,每吨按 元收取; 超过 5 吨的部分,每吨按 元收取;
(2)当 x>5 时,求 y 与 x 的函数关系式;
(3)若某个家庭有 5 人,五月份的生活用水费共 76 元,则该家庭这个月用了多少吨生活用水?
【答案】(1)1.6; 2.4;(2) y= ![]() x﹣4;(3) 该家庭这个月用了 40 吨生活用水.
x﹣4;(3) 该家庭这个月用了 40 吨生活用水.
【解析】
(1)分析图像可得答案;
(2) 当x>5时设y=kx+b,代入(5,8)、(10,20)可得一次函数解析式;
(3)把 y=![]() 代入 y=
代入 y=![]() x﹣4 可得答案.
x﹣4 可得答案.
(1)该市人均月生活用水的收费标准是:不超过 5 吨,每吨按 1.6 元收取;
超过 5 吨的部分,每吨按 2.4 元收取; 故答案为:1.6;2.4;
(2)当 x>5 时,设 y=kx+b,代入(5,8)、(10,20)得
![]() ,
,
解得 k=![]() ,b=﹣4,
,b=﹣4,
∴y= ![]() x﹣4;
x﹣4;
(3)把 y=![]() 代入 y=
代入 y=![]() x﹣4 得
x﹣4 得
![]() x﹣4=
x﹣4=![]() , 解得 x=8,
, 解得 x=8,
5×8=40(吨).
答:该家庭这个月用了 40 吨生活用水.


科目:初中数学 来源: 题型:
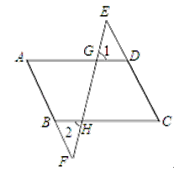
【题目】如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD∥BC和AB∥CD.
请完成下面的推理过程,并填空(理由或数学式):
∵∠1=∠2( )
∠1=∠AGH( )
∴∠2=∠AGH( )
∴AD∥BC( )
∴∠ADE=∠C( )
∵∠A=∠C( )
∴∠ADE=∠A
∴AB∥CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,那么△A2B2C2的面积是( )
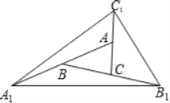
A. 7 B. 14 C. 49 D. 50
查看答案和解析>>
科目:初中数学 来源: 题型:
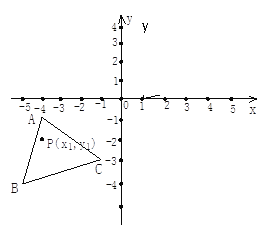
【题目】如图, 已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请在图中作出△A′B′C′;(2)写出点A′、B′、C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
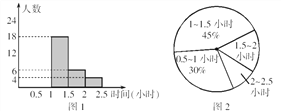
【题目】为了减轻学生的作业负担,教育局规定:初中学段学生每晚的作业总量不超过1.5小时,九(1)班学习委员亮亮对本班每位同学晚上完成作业的时间进行了一次统计,并根据收集的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题:
(1)该班共有多少名学生?将图1的条形图补充完整;
(2)计算出作业完成时间在1.5~2小时的部分对应的扇形圆心角;
(3)如果九年级共有500名学生,请估计九年级学生完成作业时间超过1.5小时的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠C,AD⊥BE于点F,BC⊥BE,点E,D,C在同一条直线上.
(1)判断AB与CD的位置关系,并说明理由;
(2)若∠ABC=120°,求∠BEC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下面题目的解答,如图,直线AB、CD被直线EF所截,H为CD与EF的交点,∠1=![]() ,∠2=
,∠2=![]() ,GH⊥CD,垂足为H.
,GH⊥CD,垂足为H.

解:因为GH⊥CD(已知),
所以∠2+∠3= (垂直的定义).
因为∠2=![]() (已知),
(已知),
所以∠3=![]() =
=![]() .
.
所以∠3=∠4=![]() ( ),
( ),
又因为∠1=![]() (已知),
(已知),
所以∠1=∠4,
所以AB∥ ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
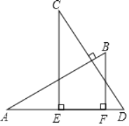
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com