
ЁОЬтФПЁПФГаЁЧјгавЛАыОЖЮЊ8mЕФдВаЮХчЫЎГиЃЌХчЫЎГиЕФжмБпгавЛШІХчЫЎЭЗЃЌХчГіЕФЫЎжљЮЊХзЮяЯпЃЎдкОрЫЎГижааФ3mДІДяЕНзюИпЃЌИпЖШЮЊ5mЃЌЧвИїИіЗНЯђХчГіЕФЫЎжљЧЁКУдкХчЫЎГижааФЕФзАЪЮЮяДІЛуКЯЃЎвдЫЎЦНЗНЯђЮЊxжсЃЌХчЫЎГижааФЮЊдЕуНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЎ
ЃЈ1ЃЉЧѓЫЎжљЫљдкХзЮяЯпЖдгІЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЭѕЪІИЕдкХчЫЎГиЮЌаоЩшБИЦкМфЃЌХчЫЎЙмвтЭтХчЫЎЃЌЮЊСЫВЛБЛСмЪЊЃЌЩэИп1.8mЕФЭѕЪІИЕеОСЂЪББиаыдкРыЫЎГижааФЖрЩйУзвдФкЃП

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ7УзЃЎ
ЃЛЃЈ2ЃЉ7УзЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЖЅЕузјБъПЩЩшЖўДЮКЏЪ§ЕФЖЅЕуЪНЃЌДњШыЕуЃЈ8ЃЌ0ЃЉЃЌЧѓГіaжЕЃЌДЫЬтЕУНтЃЛ
ЃЈ2ЃЉРћгУЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїЃЌЧѓГіЕБy=1.8ЪБxЕФжЕЃЌгЩДЫМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЩшЫЎжљЫљдкХзЮяЯпЃЈЕквЛЯѓЯоВПЗжЃЉЕФКЏЪ§БэДяЪНЮЊy=aЃЈxЉ3ЃЉ2+5ЃЈaЁй0ЃЉЃЌ
НЋЃЈ8ЃЌ0ЃЉДњШыy=aЃЈxЉ3ЃЉ2+5ЃЌЕУЃК25a+5=0ЃЌ
НтЕУЃКa=Љ![]() ЃЌ
ЃЌ
ЁрЫЎжљЫљдкХзЮяЯпЕФКЏЪ§БэДяЪНЮЊy=Љ![]() ЃЈxЉ3ЃЉ2+5ЃЈ0ЃМxЃМ8ЃЉЃЎ
ЃЈxЉ3ЃЉ2+5ЃЈ0ЃМxЃМ8ЃЉЃЎ
ЃЈ2ЃЉЕБy=1.8ЪБЃЌгаЉ![]() ЃЈxЉ3ЃЉ2+5=1.8ЃЌ
ЃЈxЉ3ЃЉ2+5=1.8ЃЌ
НтЕУЃКx1=Љ1ЃЌx2=7ЃЌ
ЁрЮЊСЫВЛБЛСмЪЊЃЌЩэИп1.8УзЕФЭѕЪІИЕеОСЂЪББиаыдкРыЫЎГижааФ7УзвдФкЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§бЇПЮЭтаЫШЄаЁзщЕФЭЌбЇУЧвЊВтСПБЛГиЬСЯрИєЕФСНПУЪїAЃЌBЕФОрРыЃЌЫћУЧЩшМЦСЫШчЭМЕФВтСПЗНАИЃКДгЪїAбизХДЙжБгкABЕФЗНЯђзпЕНEЃЌдйДгEбизХДЙжБгкAEЕФЗНЯђзпЕНFЃЌCЮЊAEЩЯвЛЕуЃЌЦфжа4ЮЛЭЌбЇЗжБ№ВтЕУЫФзщЪ§ОнЃКЂйACЃЌЁЯACBЃЛЂкEFЃЌDEЃЌADЃЛЂлCDЃЌЁЯACBЃЌЁЯADBЃЛЂмЁЯFЃЌЁЯADBЃЌFBЃЎЦфжаФмИљОнЫљВтЪ§ОнЧѓЕУAЃЌBСНЪїОрРыЕФгаЃЈ ЃЉ

A.1зщB.2зщC.3зщD.4зщ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЖЏЕу
ЃЌЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌдк
ГіЗЂЃЌдк![]() БпЩЯвдУПУы2
БпЩЯвдУПУы2![]() ЕФЫйЖШЯђЕу
ЕФЫйЖШЯђЕу![]() дШЫйдЫЖЏЃЌЭЌЪБЖЏЕу
дШЫйдЫЖЏЃЌЭЌЪБЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂЃЌдк
ГіЗЂЃЌдк![]() БпЩЯвдУПУы
БпЩЯвдУПУы![]()
![]() ЕФЫйЖШЯђЕу
ЕФЫйЖШЯђЕу![]() дШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ
дШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ![]() (
(![]() )ЃЌСЌНг
)ЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉШє![]() гы
гы![]() ЯрЫЦЃЌЧѓ
ЯрЫЦЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЕБ![]() ЮЊКЮжЕЪБЃЌЫФБпаЮ
ЮЊКЮжЕЪБЃЌЫФБпаЮ![]() ЕФУцЛ§зюаЁЃПВЂЧѓГізюаЁжЕЃЎ
ЕФУцЛ§зюаЁЃПВЂЧѓГізюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
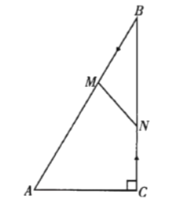
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гыxжсЯрНЛгк
гыxжсЯрНЛгк![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓВрЃЉЃЌгы
ЕФзѓВрЃЉЃЌгы![]() жсЯрНЛгкЕу
жсЯрНЛгкЕу![]() ЃЎ
ЃЎ![]() ЮЊХзЮяЯпЩЯвЛЕуЃЌКсзјБъЮЊ
ЮЊХзЮяЯпЩЯвЛЕуЃЌКсзјБъЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
ЂХЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЂЦЕБЕу![]() ЮЛгк
ЮЛгк![]() жсЯТЗНЪБЃЌЧѓ
жсЯТЗНЪБЃЌЧѓ![]() УцЛ§ЕФзюДѓжЕЃЛ
УцЛ§ЕФзюДѓжЕЃЛ
ЂЧЩшДЫХзЮяЯпдкЕу![]() гыЕу
гыЕу![]() жЎМфВПЗжЃЈКЌЕу
жЎМфВПЗжЃЈКЌЕу![]() КЭЕу
КЭЕу![]() ЃЉзюИпЕугызюЕЭЕуЕФзнзјБъжЎВюЮЊ
ЃЉзюИпЕугызюЕЭЕуЕФзнзјБъжЎВюЮЊ![]() ЃЎ
ЃЎ
ЂйЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСП
ЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЂкЕБ![]() ЪБЃЌжБНгаДГі
ЪБЃЌжБНгаДГі![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
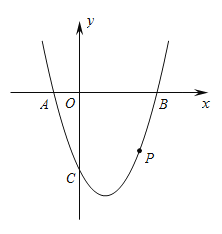
ЁОЬтФПЁПШчЭМ1ЃЌЖдГЦжсЮЊжБЯпx=![]() ЕФХзЮяЯпОЙ§BЃЈ2ЃЌ0ЃЉЁЂCЃЈ0ЃЌ4ЃЉСНЕуЃЌХзЮяЯпгыxжсЕФСэвЛНЛЕуЮЊA
ЕФХзЮяЯпОЙ§BЃЈ2ЃЌ0ЃЉЁЂCЃЈ0ЃЌ4ЃЉСНЕуЃЌХзЮяЯпгыxжсЕФСэвЛНЛЕуЮЊA
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPЮЊЕквЛЯѓЯоФкХзЮяЯпЩЯЕФвЛЕуЃЌЩшЫФБпаЮCOBPЕФУцЛ§ЮЊSЃЌЧѓSЕФзюДѓжЕЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєMЪЧЯпЖЮBCЩЯвЛЖЏЕуЃЌдкxжсЪЧЗёДцдкетбљЕФЕуQЃЌЪЙЁїMQCЮЊЕШбќШ§НЧаЮЧвЁїMQBЮЊжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЕуCбизХФГЬѕТЗОЖдЫЖЏЃЌвдЕуCЮЊа§зЊжааФЃЌНЋЕуAЃЈ0ЃЌ4ЃЉФцЪБеыа§зЊ90ЁуЕНЕуBЃЈmЃЌ1ЃЉЃЌШєЉ5ЁмmЁм5ЃЌдђЕуCдЫЖЏЕФТЗОЖГЄЮЊ__ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
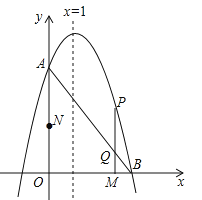
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() гыyжсЯрНЛгкЕуAЃЈ0ЃЌ3ЃЉЃЌгыxе§АыжсЯрНЛгкЕуBЃЌЖдГЦжсЪЧжБЯпx=1ЃЎ
гыyжсЯрНЛгкЕуAЃЈ0ЃЌ3ЃЉЃЌгыxе§АыжсЯрНЛгкЕуBЃЌЖдГЦжсЪЧжБЯпx=1ЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНвдМАЕуBЕФзјБъЃЎ
ЃЈ2ЃЉЖЏЕуMДгЕуOГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиxжсе§ЗНЯђдЫЖЏЃЌЭЌЪБЖЏЕуNДгЕуOГіЗЂЃЌвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШбиyжсе§ЗНЯђдЫЖЏЃЌЕБNЕуЕНДяAЕуЪБЃЌMЁЂNЭЌЪБЭЃжЙдЫЖЏЃЎЙ§ЖЏЕуMзїxжсЕФДЙЯпНЛЯпЖЮABгкЕуQЃЌНЛХзЮяЯпгкЕуPЃЌЩшдЫЖЏЕФЪБМфЮЊtУыЃЎ
ЂйЕБtЮЊКЮжЕЪБЃЌЫФБпаЮOMPNЮЊОиаЮЃЎ
ЂкЕБtЃО0ЪБЃЌЁїBOQФмЗёЮЊЕШбќШ§НЧаЮЃПШєФмЃЌЧѓГіtЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЯТСаЗНГЬ
ЃЈ1ЃЉ3ЃЈxЉ2ЃЉ2Љ12ЃН0
ЃЈ2ЃЉЃЈxЉ1ЃЉЃЈx+3ЃЉЃНЉ4
ЃЈ3ЃЉx2Љ4![]() x+1ЃН0
x+1ЃН0
ЃЈ4ЃЉЃЈ2xЉ1ЃЉЃН2ЃЈ1Љ2xЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮ![]() жаЃЌAB=8ЃЌBC=6ЃЌЙ§ЖдНЧЯп
жаЃЌAB=8ЃЌBC=6ЃЌЙ§ЖдНЧЯп![]() жаЕу
жаЕу![]() ЕФжБЯпЗжБ№НЛ
ЕФжБЯпЗжБ№НЛ![]() ЃЌ
ЃЌ![]() БпгкЕу
БпгкЕу![]() ЃЌ
ЃЌ![]() .
.
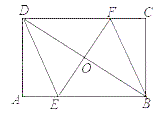
(1)ЧѓжЄЃКЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЛ
ЪЧЦНааЫФБпаЮЃЛ
(2)ЕБЫФБпаЮ![]() ЪЧСтаЮЪБЃЌЧѓ
ЪЧСтаЮЪБЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com