
分析 首先利用完全平方公式因式分解,进一步利用非负数的性质求得a、b,估算得出c的数值,进一步代入求得答案即可.
解答 解:∵$\sqrt{{a}^{2}-2\sqrt{3}a+3}$+b2+2b+1=0,
∴$\sqrt{(a-\sqrt{3})^{2}}$+(b+1)2=0,
解得:a=$\sqrt{3}$,b=-1,
∵c等于$\sqrt{17}$的小数部分,
∴c=$\sqrt{17}$-4,
∴${a^2}+\frac{1}{a^2}+\frac{1}{c}-|{-b}|$
=3+$\frac{1}{3}$+$\sqrt{17}$+4-1
=$\frac{19}{3}$+$\sqrt{17}$.
点评 此题考查配方法的运用,非负数的性质,掌握完全平方公式是解决问题的关键.


科目:初中数学 来源: 题型:选择题
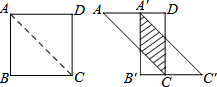 如图,将边长为12cm的正方形纸片ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分(见图中阴影)的面积为32cm2,则它移动的距离AA′等于( )
如图,将边长为12cm的正方形纸片ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分(见图中阴影)的面积为32cm2,则它移动的距离AA′等于( )| A. | 6cm | B. | 8cm | C. | 6cm或8cm | D. | 4cm或8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
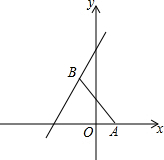 如图,点A的坐标为(1,0),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$.
如图,点A的坐标为(1,0),点B在直线y=2x+4上运动,当线段AB最短时,AB的长度为$\frac{6}{5}$$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com