
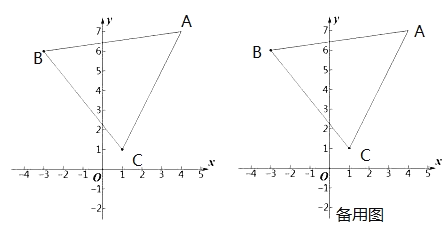
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() 其中
其中![]() 满足:
满足:![]() .
.
(1)![]()
(2)在坐标平面内,将△ABC平移,点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,若平移后E、F两点都在坐标轴上,请直接写出点E的坐标;
(3)若在△ABC内部的![]() 轴上存在一点P,在(2)的平移下,点P的对应点为点Q,使得△APQ的面积为10,则点P的坐标为_________.
轴上存在一点P,在(2)的平移下,点P的对应点为点Q,使得△APQ的面积为10,则点P的坐标为_________.
【答案】(1)b=-3,c=1;(2)E(-4,0)或E(0,5);(3)P的坐标为(0,3)或(0,![]() ).
).
【解析】
(1)根据几个非负数和的性质得到b+3=0,c﹣1=0,解方程即可得到结论;
(2)分两种情况讨论:①若B在x轴上,C在y轴上;②若B在y轴上,C在x轴上.根据B、C平移后的点的特征,得出平移方式,即可得出结论;
(3)设P(0,y),其中(1<y<7),根据(2)的两种平移方式分别得出Q的坐标,用割补法求△APQ的面积即可.
(1)由题意得:![]() ,解得:
,解得:![]() ,∴b=-3,c=1.
,∴b=-3,c=1.
(2)∵b=-3,c=1,∴B(-3,6),C(1,1).分两种情况讨论:
①若E在x轴上,F在y轴上,设B(-3,6)平移后为E(a,0),C(1,1)平移后为F(0,b),则平移方式为左1下6,∴E(-4,0);
②若E在y轴上,F在x轴上,设B(-3,6)平移后为E(0,a),C(1,1)平移后为F(b,0),则平移方式为右3下1,∴E(0,5).
综上所述:E(-4,0)或E(0,5).
(3)设P(0,y),其中(1<y<7).分两种情况讨论:
①若平移方式为左1下6,则Q(-1,y-6),如图1.
∵![]() ,∴
,∴![]() =10,解得:y=3,∴P(0,3);
=10,解得:y=3,∴P(0,3);

②若平移方式为右3下1,则Q(3,y-1),如图2.
∵![]() ,阿∴
,阿∴![]() =10,解得:y=
=10,解得:y=![]() ,∴P(0,
,∴P(0,![]() ).
).
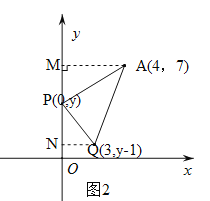
综上所述:P的坐标为(0,3)或(0,![]() ).
).


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y= ![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).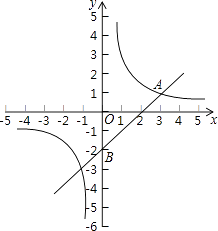
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
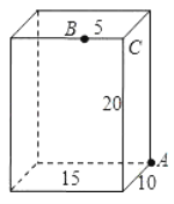
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图中,每个正方形由边长为1的小正方形组成: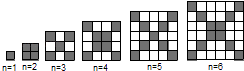
(1)观察图形,请填写下列表格:
正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
黑色小正方形个数 |
正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
黑色小正方形个数 |
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1 , 白色小正方形的个数为P2 , 问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是用4个全等的小长方形与1个小正方形密铺而成的正方形图案.已知该图案的面积为49,小正方形的面积为4,若分别用x,y(x >y)表示小长方形的长和宽,则下列关系式中不正确的是( )

A. x+y=7 B. x-y=2 C. x2 +y2=25 D. 4xy+4=49
查看答案和解析>>
科目:初中数学 来源: 题型:
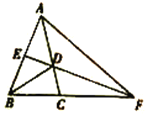
【题目】如图,在△ABC中.AB=AC.∠BAC=36°.BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF.求证:(1)EF⊥AB; (2)△ACF为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
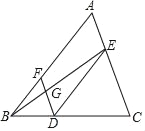
【题目】完成下面的证明:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A=∠CED( )
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( )
∴DF∥AE( )
∴∠EGF+∠AEG=180°( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,点A、B、C、D在一条直线上,填写下列空格:
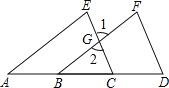
因为∠1=∠E(已知),所以______ // ______ .
因为CE//DF(已知),所以∠1=∠ ______ ,所以∠E=∠ ______ .
(2)说出(1)的推理中应用了哪两个互逆的真命题?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com