
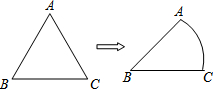
 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的$\widehat{AC}$,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )| A. | ($\frac{60}{π}$)° | B. | ($\frac{90}{π}$)° | C. | ($\frac{120}{π}$)° | D. | ($\frac{180}{π}$)° |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
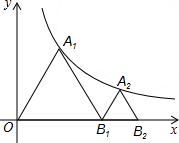 如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )
如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )| A. | (4,0) | B. | (4$\sqrt{2}$,0) | C. | (6,0) | D. | (6$\sqrt{2}$,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
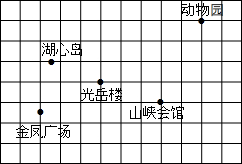 如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置.
如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
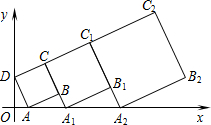 在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )| A. | 20×($\frac{3}{2}$)4030 | B. | 20×($\frac{3}{2}$)4032 | C. | 20×($\frac{3}{2}$)2016 | D. | 20×($\frac{3}{2}$)2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 科目 | 篮球 | 围棋 | 剪纸 | 舞台剧 | 茶艺 | 交谊舞 | 其它课 |
| 计数 | 正正 | 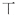 | 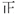 | 正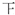 | 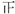 | 正一 | 正一 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
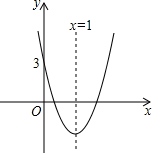 如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:| A. | ②③④ | B. | ①②③ | C. | ②③ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com