
分析 首先设飞机在无风时的飞行速度为x千米/时,则飞机顺风飞行的速度为(x+24)千米/时,逆风飞行的速度为 (x-24)千米/时,由题意得等量关系:顺风飞行速度×顺风飞行时间=逆风飞行速度×逆风飞行时间,根据等量关系列出方程,再解即可.
解答 解:设飞机在无风时的飞行速度为x千米/时,则飞机顺风飞行的速度为(x+24)千米/时,逆风飞行的速度为 (x-24)千米/时,由题意得:
$\frac{23}{12}$(x+24)=2(x-24),
解得:x=1128,
2×(1128-24)=2248(千米).
答:甲、乙两城市之间的飞行路程为2248千米.
点评 此题主要考查了一元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
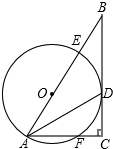 知图,在Rt△ABC中,∠C=90°,AC=12,BC=16,∠BAC的平分线交BC于D,经过A、D的⊙O交AB于E,并且点O在AB上.
知图,在Rt△ABC中,∠C=90°,AC=12,BC=16,∠BAC的平分线交BC于D,经过A、D的⊙O交AB于E,并且点O在AB上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com