
ΓΨΧβΡΩΓΩΦΈΦΈ≤ΈΦ”ΜζΤς»Υ…ηΦΤΜνΕ·Θ§–η≤ΌΩΊΜζΤς»Υ‘Ύ5ΓΝ5ΒΡΤε≈ΧΗώ…œ¥”AΒψ––ΉΏ÷ΝBΒψΘ§«“ΟΩΗω–ΓΖΫΗώΫ‘ΈΣ’ΐΖΫ–ΈΘ§÷ςΑλΒΞΈΜΙφΕ®ΝΥ»ΐΧθ––ΉΏ¬ΖΨΕR1Θ§R2Θ§R2Θ§Τδ––Ψ≠ΈΜ÷Ο»γΆΦ”κ±μΥυ ΨΘΚ
¬ΖΨΕ | ±ύΚ≈ | ΆΦάΐ | ––ΨΕΈΜ÷Ο |
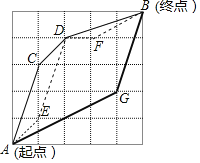
ΒΎ“ΜΧθ¬ΖΨΕ | R1 | Γ≠ | AΓζCΓζDΓζB |
ΒΎΕΰΧθ¬ΖΨΕ | R2 | Γ≠ | AΓζEΓζDΓζFΓζB |
ΒΎ»ΐΧθ¬ΖΨΕ | R3 | Γ≠ | AΓζGΓζB |
“―÷ΣA,B,C,D,E,F,GΤΏΒψΫ‘¬δ‘ΎΗώœΏΒΡΫΜΒψ…œΘ§«“ΝΫΒψ÷°ΦδΒΡ¬ΖΨΕΫ‘ΈΣœΏΕΈ.
(1)Ζ÷±πΦΤΥψ≥ω»ΐΧθ¬ΖΨΕΒΡ≥Λ;
(2)Ήν≥ΛΒΡ¬ΖΨΕ «______ (–¥≥ω±ύΚ≈)Θ§ΉνΕΧΒΡ¬ΖΨΕ « _______(–¥≥ω±ύΚ≈).
 Κ°ΦΌΧλΒΊ÷Ί«λ≥ωΑφ…γœΒΝ–¥πΑΗ
Κ°ΦΌΧλΒΊ÷Ί«λ≥ωΑφ…γœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏy=©¹x+1”κx÷αΘ§y÷αΖ÷±πΫΜ”ΎBΘ§AΝΫΒψΘ§Ε·ΒψP‘ΎœΏΕΈAB…œ“ΤΕ·Θ§“‘PΈΣΕΞΒψΉςΓœOPQ=45ΓψΫΜx÷α”ΎΒψQΘ°

Θ®1Θ©«σΒψAΚΆΒψBΒΡΉχ±ξΘΜ
Θ®2Θ©±»ΫœΓœAOP”κΓœBPQΒΡ¥σ–ΓΘ§ΥΒΟςάμ”…Θ°
Θ®3Θ© «Ζώ¥φ‘ΎΒψPΘ§ ΙΒΟΓςOPQ «Β»―ϋ»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫΪœ¬Ν–Ης ΐΧν»κœύ”ΠΒΡΦ·ΚœΡΎΘΚ
![]() Θ§1.010010001Θ§
Θ§1.010010001Θ§![]() Θ§22Θ§Θ≠8Θ§
Θ§22Θ§Θ≠8Θ§![]() Θ§Θ≠1.232232223Γ≠Θ§Θ≠1.414Θ§0Θ°
Θ§Θ≠1.232232223Γ≠Θ§Θ≠1.414Θ§0Θ°
’ΐ ΐΦ·ΚœΘϊΓΓΓΓΓΓΓΓ Γ≠Γ≠Θΐ
ΗΚ ΐΦ·ΚœΘϊΓΓΓΓΓΓΓΓ Γ≠Γ≠Θΐ
”–άμ ΐΦ·ΚœΘϊΓΓΓΓΓΓΓΓ Γ≠Γ≠Θΐ
Έόάμ ΐΦ·ΚœΘϊΓΓΓΓ ΓΓΓΓ ΓΓΓΓΓΓ Γ≠Γ≠Θΐ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy=ax2+bx+3Ψ≠ΙΐΒψ BΘ®©¹1Θ§0Θ©Θ§CΘ®2Θ§3Θ©Θ§≈ΉΈοœΏ”κy÷αΒΡΫΙΒψAΘ§”κx÷αΒΡΝμ“ΜΗωΫΙΒψΈΣDΘ§ΒψMΈΣœΏΕΈAD…œΒΡ“ΜΕ·ΒψΘ§…ηΒψMΒΡΚαΉχ±ξΈΣtΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©ΙΐΒψMΉςy÷αΒΡΤΫ––œΏΘ§ΫΜ≈ΉΈοœΏ”ΎΒψPΘ§…ηœΏΕΈPMΒΡ≥ΛΈΣ1Θ§Β±tΈΣΚΈ÷Β ±Θ§1ΒΡ≥ΛΉν¥σΘ§≤Δ«σΉν¥σ÷ΒΘΜΘ®œ»ΗυΨίΧβΡΩΜ≠ΆΦΘ§‘ΌΦΤΥψΘ©
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§Β±tΈΣΚΈ÷Β ±Θ§ΓςPADΒΡΟφΜΐΉν¥σΘΩ≤Δ«σΉν¥σ÷ΒΘΜ
Θ®4Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§ «Ζώ¥φ‘ΎΒψPΘ§ ΙΓςPADΈΣ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§÷±Ϋ”–¥≥ωtΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ ΐ÷α…œ»ΐΒψMΘ§OΘ§NΕ‘”ΠΒΡ ΐΖ÷±πΈΣΘ≠3Θ§0Θ§1Θ§ΒψPΈΣ ΐ÷α…œ»Έ“β“ΜΒψΘ§ΤδΕ‘”ΠΒΡ ΐΈΣxΘ°
(1)»γΙϊΒψPΒΫΒψMΘ§ΒψNΒΡΨύάκœύΒ»Θ§Ρ«Ο¥xΒΡ÷Β «______ΘΜ
(2) ΐ÷α…œ «Ζώ¥φ‘ΎΒψPΘ§ ΙΒψPΒΫΒψMΘ§ΒψNΒΡΨύάκ÷°ΚΆ «5ΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωxΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
(3)»γΙϊΒψP“‘ΟΩΖ÷÷”3ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»¥”ΒψOœρΉσ‘ΥΕ· ±Θ§ΒψMΚΆΒψNΖ÷±π“‘ΟΩΖ÷÷”1ΗωΒΞΈΜ≥ΛΕ»ΚΆΟΩΖ÷÷”4ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»“≤œρΉσ‘ΥΕ·Θ§«“»ΐΒψΆ§ ±≥ωΖΔΘ§Ρ«Ο¥ΦΗΖ÷÷” ±ΒψPΒΫΒψMΘ§ΒψNΒΡΨύάκœύΒ».Θ®÷±Ϋ”–¥≥ω¥πΑΗΘ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎABCD÷– ΙΐΒψAΉςAEΓΆDCΘ§¥ΙΉψΈΣEΘ§Ν§Ϋ”BEΘ§FΈΣBE…œ“ΜΒψΘ§«“ΓœAFE=ΓœDΘ°
Θ®1Θ©«σ÷ΛΘΚΓςABFΓΉΓςBECΘΜ
Θ®2Θ©»τAD=5Θ§AB=8Θ§sinD=![]() Θ§«σAFΒΡ≥ΛΘ°
Θ§«σAFΒΡ≥ΛΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓθABCD÷–Θ§EΓΔF «Ε‘Ϋ«œΏBD…œ≤ΜΆ§ΒΡΝΫΒψΘ§œ¬Ν–ΧθΦΰ÷–Θ§≤ΜΡήΒΟ≥ωΥΡ±Ώ–ΈAECF“ΜΕ®ΈΣΤΫ––ΥΡ±Ώ–ΈΒΡ «Θ® Θ©
A. BE=DF B. AE=CF C. AF//CE D. ΓœBAE=ΓœDCF
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§E «ADΒΡ÷–ΒψΘ§―”≥ΛCEΘ§BAΫΜ”ΎΒψFΘ§Ν§Ϋ”ACΘ§DFΘ°
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈACDF «ΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®2Θ©Β±CFΤΫΖ÷ΓœBCD ±Θ§–¥≥ωBC”κCDΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥±®…γΈΣΝΥΫβ –ΟώΕ‘ΓΑ…γΜα÷ς“εΚΥ–ΡΦέ÷ΒΙέΓ±ΒΡ÷Σœΰ≥ΧΕ»Θ§≤…»ΓΥφΜζ≥ι―υΒΡΖΫ ΫΫχ––Έ ΨμΒς≤ιΘ§Βς≤ιΫαΙϊΖ÷ΈΣΓΑA.Ζ«≥ΘΝΥΫβΓ±ΓΔΓΑB.ΝΥΫβΓ±ΓΔΓΑC.Μυ±ΨΝΥΫβΓ±»ΐΗωΒ»ΦΕΘ§≤ΔΗυΨίΒς≤ιΫαΙϊΜφ÷ΤΝΥ»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ°
(1)’β¥ΈΒς≤ιΒΡ –Οώ»Υ ΐΈΣ________»ΥΘ§mΘΫ________Θ§nΘΫ________ΘΜ
(2)≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
(3)»τΗΟ –‘Φ”– –Οώ100000»ΥΘ§«κΡψΗυΨί≥ι―υΒς≤ιΒΡΫαΙϊΘ§ΙάΦΤΗΟ –¥σ‘Φ”–Εύ…Ό»ΥΕ‘ΓΑ…γΜα÷ς“εΚΥ–ΡΦέ÷ΒΙέΓ±¥οΒΫΓΑA.Ζ«≥ΘΝΥΫβΓ±ΒΡ≥ΧΕ»Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com