
【题目】如图,直线y1=-x+4与双曲线y=![]() (k≠0)交于A、B两点,点A的坐标为(1,m),经过点A的直线y2=x+b与x轴交于点C.
(k≠0)交于A、B两点,点A的坐标为(1,m),经过点A的直线y2=x+b与x轴交于点C.
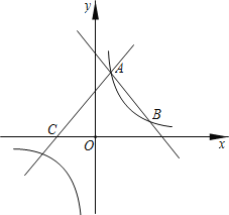
(1)求反比例函数的表达式以及点C的坐标;
(2)点P是x轴上一动点,连接AP,若△ACP是△AOB的面积的一半,求此时点P的坐标.
【答案】(1)y=![]() ,C(-2,0);(2)P点为(-
,C(-2,0);(2)P点为(-![]() ,0)或(-
,0)或(-![]() ,0).
,0).
【解析】
(1)把A(1,m)代入y1=-x+4中,求出m的值,即可求出点A的坐标,从而求出反比例函数的解析式和直线AC的解析式,联立反比例和BC直线解析式,即可求出点C的坐标;
(2)连接OA、OB,分别作AM⊥x轴于M,BN⊥x轴于N,求出△AOB的面积,设P(x,0),根据△ACP是△AOB的面积的一半,列出方程求出x,即可求出P点坐标.
(1)把A(1,m)代入y1=-x+4得,m=-1+4=3,
∴A(1,3),
∵点A在双曲线y=![]() (k≠0)上,
(k≠0)上,
∴k=1×3=3,
∴反比例函数的表达式为y=![]() ,
,
∵直线y2=x+b经过点A,
∴b=2,
∴直线y2=x+2,
令y2=0,求得x=-2,
∴C(-2,0);
(2)连接OA、OB,分别作AM⊥x轴于M,BN⊥x轴于N,
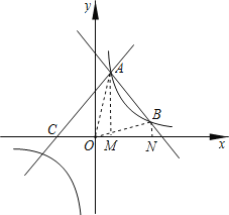
由题意得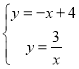 ,
,
解得![]() 或
或![]() ,
,
∴A(1,3),B(3,1),
∴AM=3,BN=1,MN=2,
∴S△AOB=S△AOM+S梯形AMNB-S△BON=S梯形AMNB=![]() =4,
=4,
设P(x,0),
∴CP=|x+2|,
∴S△ACP=![]() =
=![]() S△AOB,
S△AOB,
∴|x+2|=![]() ,则x=±
,则x=±![]() -2,
-2,
∴x=-![]() 或-
或-![]()
∴P点为(-![]() ,0)或(-
,0)或(-![]() ,0).
,0).


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)大致的图象如图,关于该二次函数,下列说法错误的是( )
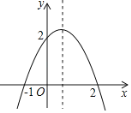
A. 函数有最大值
B. 对称轴是直线x=![]()
C. 当x<![]() 时,y随x的增大而减小
时,y随x的增大而减小
D. 当时﹣1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间准备采取每月任务定额,超产有奖的措施提高工作效率,为制定一个恰当的生产定额,从该车间200名工人中随机抽取20人统计其某月产量如下:
每人生产零件数 | 260 | 270 | 280 | 290 | 300 | 310 | 350 | 520 |
人 数 | 1 | 1 | 5 | 4 | 3 | 4 | 1 | 1 |
(1)请应用所学的统计知识.为制定生产定额的管理者提供有用的参考数据;
(2)你认为管理者将每月每人的生产定额定为多少最合适?为什么?
(3)估计该车间全年可生产零件多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
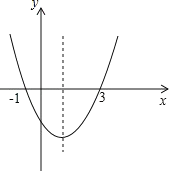
【题目】如图,二次函数 y=ax2+bx+c 的图象与 x 轴的交点的横坐标分别为-1,3,则:
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意 x 均有 ax2+bx≥a+b,其中结论正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=1,tanC=![]() ,以点A为圆心,AB长为半径作弧交AC于D,分别以B、D为圆心,以大于
,以点A为圆心,AB长为半径作弧交AC于D,分别以B、D为圆心,以大于![]() BD长为半径作弧,两弧交于点E,射线AE与BC于F,过点F作FG⊥AC于G,则FG的长为______.
BD长为半径作弧,两弧交于点E,射线AE与BC于F,过点F作FG⊥AC于G,则FG的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
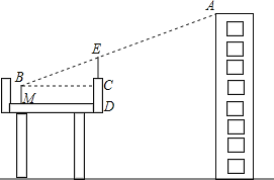
【题目】为了减轻二环高架上汽车的噪音污染,成都市政府计划在高架上的一些路段的护栏上方增加隔音屏.如图,工程人员在高架上的车道M处测得某居民楼顶的仰角∠ABC的度数是20°,仪器BM的高是0.8m,点M到护栏的距离MD的长为11m,求需要安装的隔音屏的顶部到桥面的距离ED的长(结果保留到0.1m,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
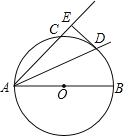
【题目】如图,AB为⊙O的直径,AC为⊙O的弦,AD平分∠BAC,交⊙O于点D,DE⊥AC,交AC的延长线于点E.
(1)求证:直线DE是⊙O的切线;
(2)若AE=8,⊙O的半径为5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的部分图象如图,则下列说法:①abc>0;②b+2a=0;③b2>4ac;④a+b+c<﹣3,正确的是( )
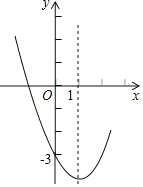
A.①②B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
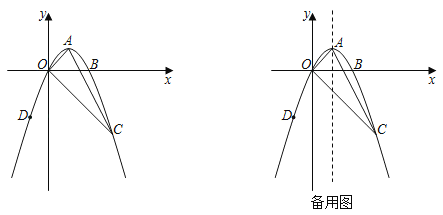
【题目】已知抛物线y=ax2+bx+c与x轴交于O、B两点,其顶点A坐标为(1,1),点C为抛物线在第四象限内的一点,其坐标为(3,﹣3).
(1)求抛物线解析式;
(2)点D为抛物线在第三象限内的一点,过点D向x轴作垂线段,垂足为H,是否存在点D使得△DHO与△AOC相似,如果存在,请求出点D坐标,如果不存在,请说明理由;
(3)点E、F分别为抛物线以及抛物线对称轴上的两动点,请问是否存在以BO为边,B、O、E、F为顶点的平行四边形,如果存在请直接写出点E坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com