
| 2 |
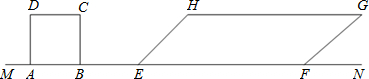
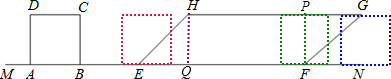 解:分别作HQ⊥EF于Q,PF⊥HG于P.
解:分别作HQ⊥EF于Q,PF⊥HG于P.| HQ |
| EH |
| 2 |
| (t-2)2 |
| 2 |
| t2-4t+4 |
| 2 |
| (6-t)2 |
| 2 |
| -t2+12t-28 |
| 2 |
| (t-8)2 |
| 2 |
| -t2+16t-56 |
| 2 |
| (12-t)2 |
| 2 |
| t2-24t+144 |
| 2 |


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
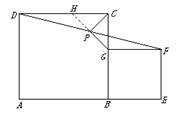 25、请阅读下列材料:
25、请阅读下列材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
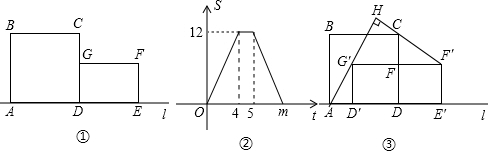
 cm,正方形ABCD以1cm/s速度向右移动,在移动过程中两图形重叠部分的面积为Scm2.试探索在不同时间内的面积S(设右移时间为t秒).
cm,正方形ABCD以1cm/s速度向右移动,在移动过程中两图形重叠部分的面积为Scm2.试探索在不同时间内的面积S(设右移时间为t秒).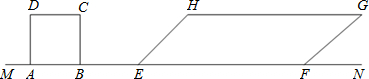
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省盐城市阜宁县古河初级中学九年级(上)第一次月考数学试卷(解析版) 题型:解答题
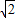 cm,正方形ABCD以1cm/s速度向右移动,在移动过程中两图形重叠部分的面积为Scm2.试探索在不同时间内的面积S(设右移时间为t秒).
cm,正方形ABCD以1cm/s速度向右移动,在移动过程中两图形重叠部分的面积为Scm2.试探索在不同时间内的面积S(设右移时间为t秒).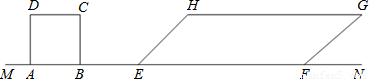
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com