

分析 (1)过点A1和任意不相邻的两点连接可得出到一条对角线;同理可得过点A2、A3的情况.
(2)过点A1的和过点A2的没有重复的,但和过点A3的有重复的(A1A3和A3A1重复);
(3)过每一点有(n-3)条对角线,除去重复的即可得出总对角线的条数.
解答 解:(1)过顶点A1可以画(n-3)条对角线,它们分别是A1An-1(n>3);过顶点A2可以画(n-3)条对角线,过顶点A3可以画(n-3)条对角线;
(2)过点A1的和过点A2的没有重复的,但和过点A3的有重复的(A1A3和A3A1重复);
(3)n边形的一个顶点不能与它本身及左右两个邻点相连成对角线,故可连出(n-3)条,
共有n个顶点,应为n(n-3)条,这样算出的数,正好多出了一倍,所以再除以2.
即n边形的对角线条数的为$\frac{n(n-3)}{2}$.
故答案为:(n-3),A1An-1(n>3),(n-3),(n-3).
点评 此题考查了多边形的对角线的知识,属于基础题,关键是熟练掌握一些基本知识.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
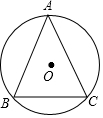 已知⊙O的半径为2,△ABC内接于⊙O,$\widehat{AB}$、$\widehat{BC}$、$\widehat{AC}$的长之比为3:2:3,求BC的长.
已知⊙O的半径为2,△ABC内接于⊙O,$\widehat{AB}$、$\widehat{BC}$、$\widehat{AC}$的长之比为3:2:3,求BC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
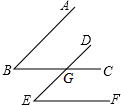 已知:①如图,AB∥DE,BC∥EF,BC与DE相交于点G.请你猜想∠B与∠E之间具有什么数量关系,并说明理由.②请猜测:如果一个角的两条边与另一个角的两条边分别平行,那么这两个角的数量关系是相等或互补.
已知:①如图,AB∥DE,BC∥EF,BC与DE相交于点G.请你猜想∠B与∠E之间具有什么数量关系,并说明理由.②请猜测:如果一个角的两条边与另一个角的两条边分别平行,那么这两个角的数量关系是相等或互补.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
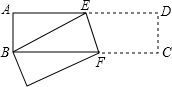 如图,已知,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )
如图,已知,矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF,则AE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com