
分析 (1)原式利用零指数幂、负整数指数幂法则,以及算术平方根定义计算即可得到结果.
(2)先把原式的分母通分,化为同分母的分数后再相加减.
(3)根据分式混合运算法则进行运算,先算乘法,再算加减.
解答 解:(1)($\frac{1}{3}$)-2-(-1)2016-$\sqrt{25}$+(π-1)0,
=32-1-5+1,
=9-5,
=4;
(2)$\frac{x}{x-1}$-$\frac{3x-1}{{x}^{2}-1}$,
=$\frac{x(x+1)}{{x}^{2}-1}$-$\frac{3x-1}{{x}^{2}-1}$,
=$\frac{{x}^{2}+x-3x+1}{{x}^{2}-1}$,
=$\frac{(x-1)^{2}}{(x-1)(x+1)}$,
=$\frac{x-1}{x+1}$;
(3)$\frac{1}{2a}$-$\frac{1}{a+b}$($\frac{a+b}{2a}$-a-b),
=$\frac{1}{2a}$-$\frac{1}{2a}$-$\frac{1}{a+b}$•(-a-b),
=1.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{3}{4}$ | C. | 0 | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
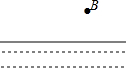 如图,B村位于一条河的一岸,现在要将河里的水通过修建水渠引到村里进行使用,问:这条水渠该如何修,才能使到A村的距离最短,请画出图形,并说明理由?(画图可借助三角板,量角器等工具)
如图,B村位于一条河的一岸,现在要将河里的水通过修建水渠引到村里进行使用,问:这条水渠该如何修,才能使到A村的距离最短,请画出图形,并说明理由?(画图可借助三角板,量角器等工具)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
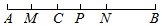 如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.
如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
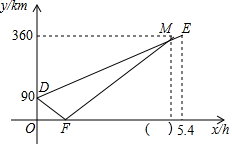 A,B,C三地在同一条公路上,A地在B,C两地之间,甲、乙两车同时从A地出发匀速行驶,甲车驶向C地,乙车先驶向B地,到达B地后,调头按原速经过A地驶向C地(调头时间忽略不计),到达C地停止行驶,甲车比乙车晚0.4小时到达C地,两车距B地的路程y(km)与行驶时间x(h)之间的函数关系如图所示,请结合图象信息,解答下列问题:
A,B,C三地在同一条公路上,A地在B,C两地之间,甲、乙两车同时从A地出发匀速行驶,甲车驶向C地,乙车先驶向B地,到达B地后,调头按原速经过A地驶向C地(调头时间忽略不计),到达C地停止行驶,甲车比乙车晚0.4小时到达C地,两车距B地的路程y(km)与行驶时间x(h)之间的函数关系如图所示,请结合图象信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com