
 ,75°),则线段AB长为 .
,75°),则线段AB长为 .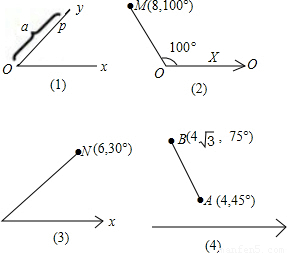
 ,∠AOB=30°过点B作BD⊥AO于点D,可得DB=2,OD=2
,∠AOB=30°过点B作BD⊥AO于点D,可得DB=2,OD=2 ,进而得到AD=2,根据勾股定理可求得AB=4.
,进而得到AD=2,根据勾股定理可求得AB=4. 解:(1)ON=6,∠XON=30°;
解:(1)ON=6,∠XON=30°; ,∠AOB=75°-45°=30°.
,∠AOB=75°-45°=30°. OB=2
OB=2 ,OD=BO•cos30°=4
,OD=BO•cos30°=4 ×
× =6.
=6. =4.
=4.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
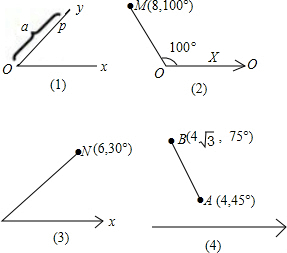 4
4| 3 |
查看答案和解析>>
科目:初中数学 来源:第7章《锐角三角函数》中考题集(23):7.5 解直角三角形(解析版) 题型:填空题
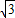 ,75°),则线段AB长为 .
,75°),则线段AB长为 .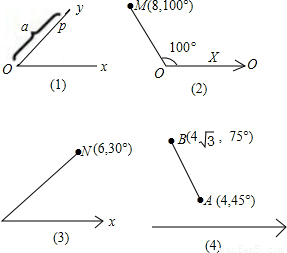
查看答案和解析>>
科目:初中数学 来源:第25章《解直角三角形》中考题集(21):25.3 解直角三角形(解析版) 题型:填空题
 ,75°),则线段AB长为 .
,75°),则线段AB长为 .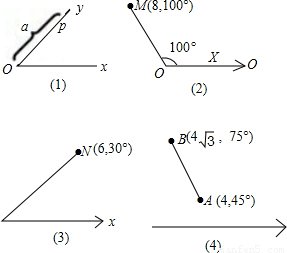
查看答案和解析>>
科目:初中数学 来源:第25章《解直角三角形》中考题集(21):25.3 解直角三角形及其应用(解析版) 题型:填空题
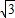 ,75°),则线段AB长为 .
,75°),则线段AB长为 .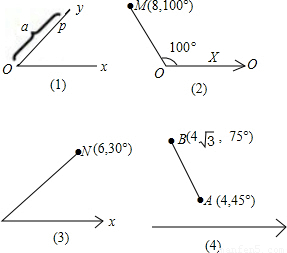
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com