
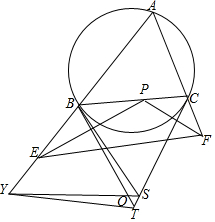
 如图,在△ABC中,∠A=60°,P为线段BC(不含端点)上一点,E、F分别为射线AB、AC上的点,且BP=BE,CP=CF,△ABC的外接圆在B、C两点处的切线交于点S.设△EPF的外心为O,BO与CS交于点T,SO与直线AB交于点Y.求证:B、Y、T、S四点共圆.
如图,在△ABC中,∠A=60°,P为线段BC(不含端点)上一点,E、F分别为射线AB、AC上的点,且BP=BE,CP=CF,△ABC的外接圆在B、C两点处的切线交于点S.设△EPF的外心为O,BO与CS交于点T,SO与直线AB交于点Y.求证:B、Y、T、S四点共圆. 分析 先判断出BS=SC,结合∠A=60°,得出∠BSC=60°,进而得出△BEO≌△BPO,即:∠OBP=$\frac{1}{2}$∠EBP,同理:∠OCB=$\frac{1}{2}$∠FCP,即可得出点B,O,S,C四点共圆,再判断出△YBO≌△CBO,得出BY=BC,进而△BYT≌△BCT,即可点B,Y,T,S四点共圆.
解答 解:如图,连接OE,OP,OC,OF,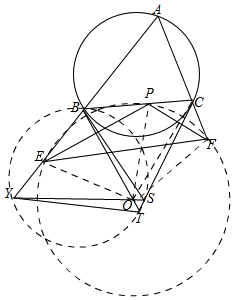
∵BS,CS是△ABC的外接圆的切线,
∴BS=SC,
∵∠A=60°,
∴∠BSC=60°(△SBC是等边三角形),
∵O为△PEF的外心,
∴OE=OP,在△BEO和△BPO中,$\left\{\begin{array}{l}{BP=BE}\\{EO=PO}\\{OB=OB}\end{array}\right.$
∴△BEO≌△BPO,
∴∠EBO=∠PBO,
∴∠OBP=$\frac{1}{2}$∠EBP,
同理:∠OCB=$\frac{1}{2}$∠FCP,
∵∠BOC=180°-∠OBP-∠OCB=180°-$\frac{1}{2}$∠EBP-$\frac{1}{2}$∠FCP=60°=∠BSC,
∴B,O,S,C四点共圆,
∴∠YOB=∠SOC=∠BOC=60°,
在△YBO和△CBO中,$\left\{\begin{array}{l}{∠YBO=∠CBO}\\{BO=BO}\\{∠BOY=∠BOC}\end{array}\right.$,
∴△YBO≌△CBO,
∴BY=BC,
在△BYT和BCT中,$\left\{\begin{array}{l}{BY=BC}\\{∠YBT=∠CBT}\\{BT=BT}\end{array}\right.$,
∴△BYT≌△BCT,
∴∠BYT=∠BCT=60°=∠BSC,
∴B,Y,T,S四点共圆.
点评 此题是四点共圆,主要考查了切线的性质,等边三角形的判定和性质,全等三角形的判定和性质,四点共圆的判定方法,解本题的关键是∠OBP=$\frac{1}{2}$∠EBP和∠OCB=$\frac{1}{2}$∠FCP,作出辅助线是解本题的难点,是一道难度不太大的很好的竞赛题.


科目:初中数学 来源: 题型:选择题
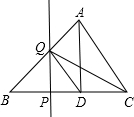 如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )
如图,△ABC中,AD⊥BC,垂足为D,AD=BD=3,CD=2,点P从点B出发沿线段BC的方向移动到点C停止,过点P作PQ⊥BC,交折线BA-AC于点Q,连接DQ、CQ,若△ADQ与△CDQ的面积相等,则线段BP的长度是( )| A. | $\frac{9}{5}$或4 | B. | $\frac{6}{5}$或4 | C. | $\frac{9}{5}$或$\frac{13}{5}$ | D. | $\frac{6}{5}$或$\frac{13}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )
如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在A′,D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,$\frac{CF}{BE}$的值为( )| A. | $\frac{3-\sqrt{3}}{2}$ | B. | $\frac{3+\sqrt{3}}{2}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\frac{3+\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
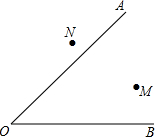 已知∠AOB,点M、N,在∠AOB的内部求作一点P.使点P到∠AOB的两边距离相等,且PM=PN(要求:尺规作图,保留作图痕迹,不写作法).
已知∠AOB,点M、N,在∠AOB的内部求作一点P.使点P到∠AOB的两边距离相等,且PM=PN(要求:尺规作图,保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线的不等式为y=-x2+6x+c.
已知抛物线的不等式为y=-x2+6x+c.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1+x)2=500 | B. | 500(1+x)2=3600 | ||
| C. | (3600-500)(1+x)=3600 | D. | (3600-500)(1+x)2=3600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com