

分析 (1)设BD于MN交于点H,如图1(1),根据正方形的性质得∠ABH=∠CBH=45°,BA=BC,由于∠MBN=45°,∠ABM=∠CBN,则∠ABM=∠HBM=∠HBN=∠CBN,再证明△ABM≌△CBN得到BM=BN,AM=CN,接着根据等腰三角形的性质可判断BH⊥MN,于是根据角平分线的性质得MA=MH,NH=NC,所以有MN=AM+CN;
(2)把△BAM绕点B顺时针旋转90°得到△BCP,如图1(2),根据旋转的性质得BM=BP,AM=CP,∠MBP=90°,∠BCP=∠A=90°,再证明点P在DC的延长线上,则NC+CP=NP,利用∠MBN=$\frac{1}{2}$∠ABC=45°得到∠NBP=45°,接着可证明△BNM≌△BNP,则MN=NP,于是有MN=CP+CN=AM+CN;
【拓展】如图2,由于∠ABC+∠ADC=180°,根据四边形内角和得到∠BAD+∠BCD=180°,则∠BAM=∠BCD,根据旋转的定义,可把△BAM绕点B顺时针旋转90°得到△BCQ,则根据旋转的性质得∠BAM=∠BCQ,BM=BQ,∠MBQ=∠ABC,则∠BCQ=∠BCD,则可判断点Q在CN上得到CN=CQ+MQ=AM+NQ,然后证明△BMN≌△BQN得到MN=QN,则CN=AM+MN.
解答 (1)解:设BD于MN交于点H,如图1(1),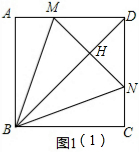
∵BD为正方形ABCD的正方形,
∴∠ABH=∠CBH=45°,BA=BC,
∵∠MBN=45°,∠ABM=∠CBN,
∴∠ABM=∠HBM=∠HBN=∠CBN,
在△ABM和△CBN中
$\left\{\begin{array}{l}{∠A=∠C}\\{AB=CB}\\{∠ABM=∠CBN}\end{array}\right.$,
∴△ABM≌△CBN,
∴BM=BN,AM=CN,
而∠HBM=∠HBN,
∴BH⊥MN,
∴MA=MH,NH=NC,
∴AM=MH=HN=NC,
∴MN=AM+CN;
故答案为③;
(2)解:在(1)中线段MN、AM、CN之间的数量关系仍然成立.理由如下:
把△BAM绕点B顺时针旋转90°得到△BCP,如图1(2),
∴BM=BP,AM=CP,∠MBP=90°,∠BCP=∠A=90°,
∵∠BCP+∠BCN=180°,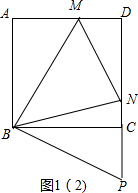
∴点P在DC的延长线上,
∴NC+CP=NP,
∵∠MBN=$\frac{1}{2}$∠ABC=45°,
∴∠NBP=45°,
在△BNM和△BNP中
$\left\{\begin{array}{l}{BM=BP}\\{∠MBN=∠PBN}\\{BN=BN}\end{array}\right.$,
∴△BNM≌△BNP,
∴MN=NP,
∴MN=CP+CN=AM+CN;
【拓展】解:如图2,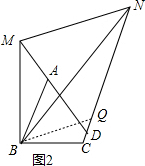 ∵∠ABC+∠ADC=180°,
∵∠ABC+∠ADC=180°,
∴∠BAD+∠BCD=180°,
而∠BAD+∠BAM=180°,
∴∠BAM=∠BCD,
∵AB=BC,
∴把△BAM绕点B顺时针旋转90°得到△BCQ,
∴∠BAM=∠BCQ,BM=BQ,∠MBQ=∠ABC,
∴∠BCQ=∠BCD,
∴点Q在CN上,
∴CN=CQ+MQ=AM+NQ,
∵∠MBN=$\frac{1}{2}$∠ABC,
∴∠MBN=$\frac{1}{2}∠$MBQ,
∴∠MBN=∠QBN,
在△BMN和△BQN中
$\left\{\begin{array}{l}{BM=BQ}\\{∠MBN=∠QBN}\\{BN=BN}\end{array}\right.$,
∴△BMN≌△BQN,
∴MN=QN,
∴CN=AM+MN,
即MN=CN-AM.
点评 本题考查了四边形的综合题:熟练掌握正方形的性质和旋转的性质;灵活应用全等三角形的判定与性质解决线段相等的问题;解决本题的关键是构建全等三角形.


科目:初中数学 来源: 题型:选择题
 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AD=AB+CD,AE平分∠BAD,下列结论:①AD=2AE;②∠ADE=∠AEB;③∠AED=90°;④S△ADE=$\frac{1}{4}$AD•BC中,一定成立的有( )
如图,点E是BC的中点,AB⊥BC,DC⊥BC,AD=AB+CD,AE平分∠BAD,下列结论:①AD=2AE;②∠ADE=∠AEB;③∠AED=90°;④S△ADE=$\frac{1}{4}$AD•BC中,一定成立的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图△ABC,△DMN中∠A=∠MDN=90°,AB=AC=4,D为BC边中点,绕D点转动△DMN.使得DM与线段AB交于E点(不与A、B重合),DN边与线段AC交于F点
如图△ABC,△DMN中∠A=∠MDN=90°,AB=AC=4,D为BC边中点,绕D点转动△DMN.使得DM与线段AB交于E点(不与A、B重合),DN边与线段AC交于F点查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=ax2+bx+c过点A(-1,0),B(4,0),C(-2,-3)三点,与y轴相交于点D.
如图,已知抛物线y=ax2+bx+c过点A(-1,0),B(4,0),C(-2,-3)三点,与y轴相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).
如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
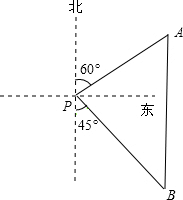 如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4.
如图,一艘海轮位于灯塔P的北偏东60°方向,距灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处距离灯塔P有多远(结果取整数).参考数值:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com