
【题目】在平面直角坐标系中,OA=4,OC=8,四边形ABCO是平行四边形.
(1)求点B的坐标及四边形ABCO的面积;
(2)若点P从点C以2单位长度/秒的速度沿CO方向移动,同时点Q从点O以1单位长度/秒的速度沿OA方向移动,设移动的时间为t秒,△AQB与△BPC的面积分别记为![]() ,
,![]() ,四边形QBPO的面积是否发生变化,若不变,求出并证明你的结论,若变化,求出变化的范围.
,四边形QBPO的面积是否发生变化,若不变,求出并证明你的结论,若变化,求出变化的范围.
(3)在(2)的条件下,是否存在某个时同,使![]() ,若存在,求出t的值,若不存在,试说明理由;
,若存在,求出t的值,若不存在,试说明理由;

【答案】(1)点B的坐标为(8,4),四边形ABCO的面积32;(2)四边形QBPO的面积不发生变化,面积为定值16,证明过程见解析;(3)存在t的值,此时![]() .
.
【解析】
(1)先证四边形ABCO是矩形,进而可根据OA=4,OC=8求得答案;
(2)由题意可知OQ=t,CP=2t,进而可用含t的代数式表示S△ABQ及S△BCP,进而可根据 S四边形QBPO=S矩形ABCO- S△ABQ- S△BCP=32-(16-4t)-4t,化简即可得到答案;
(3)由(2)可知:S△ABQ=16-4t,S四边形QBPO=16,再结合![]() 即可求得t的值.
即可求得t的值.
解:(1)∵四边形ABCO是平行四边形,∠AOC=90°,
∴四边形ABCO是矩形,
∵OA=4,OC=8,
∴点B的坐标为(8,4),S矩形ABCO=OA·OC=8×4=32,
(2)∵四边形ABCO是矩形,
∴AB=OC=8,BC=OA=4,
由题意可知:OQ=t,CP=2t,
∴AQ=OA-OQ=4-t,
∴S△ABQ=![]() AB·AQ=
AB·AQ=![]() ×8(4-t)=16-4t,
×8(4-t)=16-4t,
S△BCP=![]() BC·CP=
BC·CP=![]() ×4×2t=4t,
×4×2t=4t,
∴S四边形QBPO=S矩形ABCO-S△ABQ-S△BCP
=32-(16-4t)-4t
=32-16+4t-4t
=16,
∴四边形QBPO的面积不变,面积为16;
(3)由(2)可知:S△ABQ=16-4t,S四边形QBPO=16,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴存在t的值使得![]() ,此时
,此时![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠C=90°,∠A=30°.
(1)用直尺和圆规作AB的垂直平分线,分别交AC、AB于点E.D(保留作图痕迹,不写作法)
(2)猜想AC与CE之间的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛,各参赛选手的成绩如下(单位:分):
A班:88,91,92,93,93,93,94,98,98,100
B班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
A班 | 100 | a | 93 | 93 | c |
B班 | 99 | 95 | b | 93 | 8.4 |
(1)求表中a、b、c的值;
(2)依据数据分析表,有人说:“最高分在A班,A班的成绩比B班好”,但也有人说B班的成绩要好,请给出两条支持B班成绩好的理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数 ![]() 的图像记为
的图像记为 ![]() ,其顶点为
,其顶点为 ![]() ,二次函数
,二次函数 ![]() 的图像记为
的图像记为 ![]() ,其顶点为
,其顶点为 ![]() ,且满足点
,且满足点 ![]() 在
在 ![]() 上,点
上,点 ![]() 在
在 ![]() 上,则称这两个二次函数互为“伴侣二次函数”.
上,则称这两个二次函数互为“伴侣二次函数”.
(1)写出二次函数 ![]() 的一个“伴侣二次函数”;
的一个“伴侣二次函数”;
(2)设二次函数 ![]() 与
与 ![]() 轴的交点为
轴的交点为 ![]() ,求以点
,求以点 ![]() 为顶点的二次函数
为顶点的二次函数 ![]() 的“伴侣二次函数”;
的“伴侣二次函数”;
(3)若二次函数 ![]() 与其“伴侣二次函数”的顶点不重合,试求该“伴侣二次函数”的二次项系数.
与其“伴侣二次函数”的顶点不重合,试求该“伴侣二次函数”的二次项系数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆八中的老师工作很忙,但初一年级很多数学老师仍然坚持锻炼身体,比如张老师就经常坚持饭后走一走.某天晚饭后他从学校慢步到附近的中央公园,在公园里休息了一会后,因学校有事,快步赶回学校.下面能反映当天张老师离学校的距离y与时间x的关系的大致图象是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
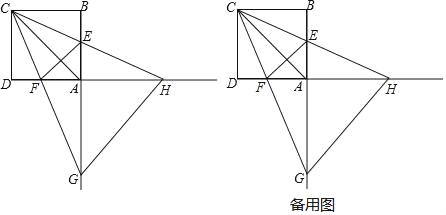
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. a6÷2a2=2a3 B. (﹣![]() xy3)2=﹣x2y5
xy3)2=﹣x2y5
C. (﹣3a2)(﹣2ab2)=6a3b2 D. (﹣5)0=﹣5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com