
【题目】如图,将一副三角板中含有30°角的三角板的直角顶点落在等腰直角三角形的斜边的中点D处,并绕点D旋转,两直角三角板的两直角边分别交于点E,F,下列结论:①DE=DF;②S四边形AEDF=S△BED+S△CFD;③S△ABC=EF2;④EF2=BE2+CF2,其中正确的序号是_____.

【答案】①②④.
【解析】
连接AD,如图,由已知条件利用ASA推导证明△DBE≌△DAF,根据全等三角形的性质可得DE=DF,由此可判断①;同①一样的道理可证明△DCF≌△DAE,由此可判断②;由S△ABC=![]() ADBC=
ADBC=![]() AD2AD=AD2,确定出只有当DE⊥AB时,四边形AEDF为矩形,此时AD=EF,由此可以判断③;在Rt△AEF中,EF2=AE2+AF2,再根据△DBE≌△DAF,△DCF≌△DAE,即可得到EF2=BE2+CF2,由此可判断④.
AD2AD=AD2,确定出只有当DE⊥AB时,四边形AEDF为矩形,此时AD=EF,由此可以判断③;在Rt△AEF中,EF2=AE2+AF2,再根据△DBE≌△DAF,△DCF≌△DAE,即可得到EF2=BE2+CF2,由此可判断④.
连接AD,如图,
∵△ABC为等腰直角三角形,
∴AB=AC,∠B=∠C=45°,
∵点D为等腰直角△ABC的斜边的中点,
∴AD⊥BC,BD=CD=AD,AD平分∠BAC,
∴∠2+∠3=90°,∠1=45°,
∵∠EDF=90°,即∠4+∠3=90°,
∴∠2=∠4,
在△DBE和△DAF中
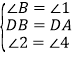 ,
,
∴△DBE≌△DAF(ASA),
∴DE=DF,所以①正确;
同理可得△DCF≌△DAE,
∴S四边形AEDF=S△BED+S△CFD,所以②正确;
∵S△ABC=![]() ADBC=
ADBC=![]() AD2AD=AD2,
AD2AD=AD2,
而只有当DE⊥AB时,四边形AEDF为矩形,此时AD=EF,
∴S△ABC不一定等于EF2,所以③错误;
在Rt△AEF中,EF2=AE2+AF2,
∵△DBE≌△DAF,△DCF≌△DAE,
∴BE=AF,CF=AE,
∴EF2=BE2+CF2,所以④正确,
故答案为:①②④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线——螺旋前进的.
通过阅读以上信息,解决下列问题:
(1)若树干的周长(即图中圆柱的底面周长)为30cm,葛藤绕一圈升高(即圆柱的高)40cm,则它爬行一圈的路程是多少?
(2)若树干的周长为80cm,葛藤绕一圈爬行100cm,它爬行10圈到达树顶,则树干高多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1个单位的正方形,A(-3,1),B(3,2),解答以下问题:
(1)在图中标出平面直角坐标系的原点O,并建立直角坐标系;
(2)点A关于x轴的对称点A’坐标为 ,并在坐标系中画出点A’;
(3)点P是x轴上一点,当PA+PB最小时,在图中画出点P的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生的学习生活,某班组织学生参观某爱国主义教育基地,所联系的旅行社收费标准如下:
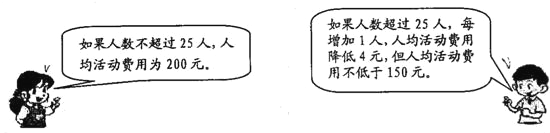
活动结束后,该班共支付给该旅行社活动费用5600元,该班共有多少人参加这次活动?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,等腰Rt△ABC,在直角边AB的左侧作直线AP,点B关于直线AP的对称点为E,连结BE,CE,其中CE交直线AP于点F.
(1)当∠PAB=29°时,求∠ACE的度数.
(2)当0°<∠PAB<45°时,利用(图1),求∠BEC度数.
(3)若45°<∠PAB<90°,用等式表示线段AB,FE,FC之间的数量关系,并证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的网格中,已知A(0,4),B(﹣2,2),C(3,0).

(1)在如图网格中画出△ABC,及△ABC关于x轴对称的△A1B1C1;
(2)写出点A1、B1、C1的坐标.
(3)求出△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com