
分析 分两种情况考虑:如图1所示,此时△ABC为锐角三角形,在直角三角形ABD与直角三角形ACD中,利用勾股定理求出AB的长即可;如图2所示,此时△ABC为钝角三角形,同理求出AB的长即可.
解答 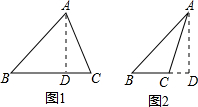 解:分两种情况考虑:
解:分两种情况考虑:
∵AC=5,BC=6,△ABC的面积为9,
∴AD=3,
如图1所示,此时△ABC为锐角三角形,
在Rt△ACD中,根据勾股定理得:DC=$\sqrt{{5}^{2}-{3}^{2}}$=4;
在Rt△ABD中,根据勾股定理得:AB=$\sqrt{A{D}^{2}+D{B}^{2}}=\sqrt{{3}^{2}+{2}^{2}}=\sqrt{13}$,
如图2所示,此时△ABC为钝角三角形,
在Rt△ACD中,根据勾股定理得:DC=$\sqrt{{5}^{2}-{3}^{2}}$=4;
在Rt△ABD中,根据勾股定理得:AB=$\sqrt{A{D}^{2}+B{D}^{2}}=\sqrt{{3}^{2}+(6+4)^{2}}=\sqrt{109}$,
故答案为:$\sqrt{13}$或$\sqrt{109}$
点评 本题考查的是勾股定理,在解答此题时要注意进行分类讨论,不要漏解.


科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$,-x,0,$\frac{4}{7}$都是单项式 | B. | 多项式3x3-2x2+x-1是三次四项式 | ||
| C. | -73的底数是-7,指数是3 | D. | 数轴上,右边的数总比左边的数大 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 17 | B. | 16 | C. | 15 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一辆汽车而经过两次拐弯之后,行驶方向与原来平行,若第一次是向左拐40°,则第二次拐弯的角度是( )
如图,一辆汽车而经过两次拐弯之后,行驶方向与原来平行,若第一次是向左拐40°,则第二次拐弯的角度是( )| A. | 右拐40° | B. | 左拐40° | C. | 左拐140° | D. | 右拐140° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com