
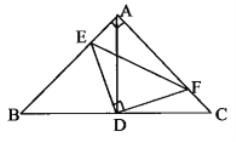
【题目】如图, 在![]() 中,
中,![]() ,
,![]() , 点
, 点![]() 为
为![]() 中点, 点
中点, 点![]() 在边
在边![]() 上, 连接
上, 连接![]() ,过点
,过点![]() 作
作
![]() 上
上![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 。下列结论:
。下列结论:
(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]()
其中正确的是__________(填写所有正确结论的序号)
【答案】![]()
【解析】
由“ASA”可证△ADE≌△CDF,可得AE=CF,S△ADE=S△CDF,由等腰直角三角形的性质可判断(1),(3),由三角形的三边关系可判断(2),由三角形面积关系可判断(4).
∵AB=AC,∠BAC=90°,点D为BC中点,
∴BD=CD=AD=![]() BC,∠BAD=∠CAD=∠C=45°,AD⊥BC,BC=
BC,∠BAD=∠CAD=∠C=45°,AD⊥BC,BC=![]() AB,
AB,
∵DF⊥DE,
∴∠EDF=∠ADC=90°,
∴∠ADE=∠CDF,且AD=CD,∠BAD=∠C,
∴△ADE≌△CDF(ASA),
∴AE=CF,
∴BE+CF=BE+AE=AB,且BC=![]() AB,
AB,
∴BE+CF=![]() BC,故(1)正确;
BC,故(1)正确;
∵AE+AF≥EF,
∴AF+CF≥EF,
∴AC≥EF,
∴![]() AD≥EF,故(2)错误;
AD≥EF,故(2)错误;
∵△ADE≌△CDF,
∴S△ADE=S△CDF,
∴S四边形AEDF=S△ADF+S△CDF=S△ADC=![]() ×AD2,故(3)正确;
×AD2,故(3)正确;
∵S△AEF=![]() ×AE×AF,且AE+AF=AC,
×AE×AF,且AE+AF=AC,
∴当AE=AF时,S△AEF的最大值=![]() S△ABC,
S△ABC,
∴S△AEF≤![]() ,故(4)正确,
,故(4)正确,
故答案为:(1) (3) (4)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
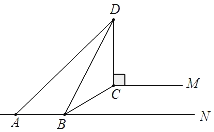
【题目】如图,BC是坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是45°和60°.
(1)求灯杆CD的高度;
(2)求AB的长度(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个矩形纸片![]() ,将该纸片放置在平面直角坐标系中,点
,将该纸片放置在平面直角坐标系中,点![]() ,点
,点![]() ,点P为
,点P为![]() 边上的动点.
边上的动点.
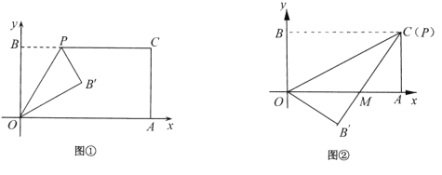
(1)如图①,经过点O、P折叠该纸片,得点![]() 和折痕
和折痕![]() .当点P的坐标为
.当点P的坐标为![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图②,当点P与点C重合时,经过点O、P折叠纸片,使点B落在点![]() 的位置,
的位置,![]() 与
与![]() 交于点M,求点M的坐标;
交于点M,求点M的坐标;
(3)过点P作直线![]() ,交
,交![]() 于点Q,再取
于点Q,再取![]() 中点T,
中点T,![]() 中点N,分别以
中点N,分别以![]() ,
,![]() ,
,![]() ,
,![]() 为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段
为折痕,依次折叠该纸片,折叠后点O的对应点与点B的对应点恰好重合,且落在线段![]() 上,A、C的对应点也恰好重合,也落在线段
上,A、C的对应点也恰好重合,也落在线段![]() 上,求此时点P的坐标(直接写出结果即可).
上,求此时点P的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
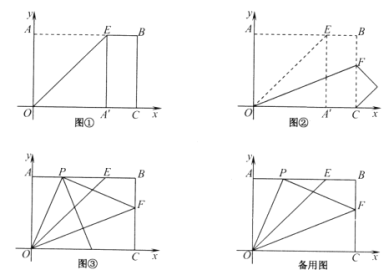
【题目】将一个矩形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() ,点
,点![]() ,点E,F分别在边
,点E,F分别在边![]() ,
,![]() 上.沿着
上.沿着![]() 折叠该纸片,使得点A落在
折叠该纸片,使得点A落在![]() 边上,对应点为
边上,对应点为![]() ,如图①.再沿
,如图①.再沿![]() 折叠,这时点E恰好与点C重合,如图②.
折叠,这时点E恰好与点C重合,如图②.
(Ⅰ)求点C的坐标;
(Ⅱ)将该矩形纸片展开,再折叠该矩形纸片,使点O与点F重合,折痕与![]() 相交于点P,展开矩形纸片,如图③.
相交于点P,展开矩形纸片,如图③.
①求![]() 的大小;
的大小;
②点M,N分别为![]() ,
,![]() 上的动点,当
上的动点,当![]() 取得最小值时,求点N的坐标(直接写出结果即可).
取得最小值时,求点N的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知等边![]() , 点
, 点![]() 在射线
在射线![]() 上(不与
上(不与![]() 重合),连接
重合),连接![]() , 将射线
, 将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() .
.
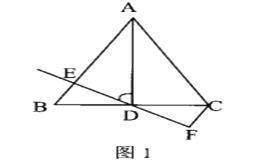
(1)如图1,当点D为线段BC中点时,请直接写出CF,BE,CD三条线段之间的数量;
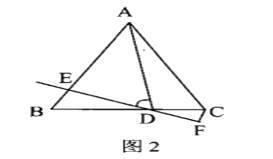
(2)如图2,“点![]() 在线段
在线段![]() 上且不是
上且不是![]() 中点时,
中点时,![]() 中结论是否成立?若成立,请说明理由。若不成立,请写出正确的结论并说明理由;
中结论是否成立?若成立,请说明理由。若不成立,请写出正确的结论并说明理由;
(3)若![]() ,当
,当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在A,B两地之间有汽车站C站,货车由A地驶往B地,客车由B地驶往C站.两车同时出发,匀速行驶.图2是货车、客车离C站的路程y1,y2(千米)与行驶时间x(小时)之间的函数关系图象.
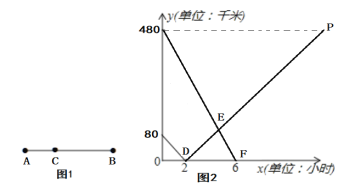
(1)填空:A,B两地相距 千米;
(2)求两小时后,货车离C站的路程y1与行驶时间x之间的函数关系式;
(3)客、货两车何时相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在绿化某县城与高速公路的连接路段中,需购买罗汉松、雪松两种树苗共400株,罗汉松树苗每株60元,雪松树苗每株70元.相关资料表明:罗汉松、雪松树苗的成活率分别为70%,90%.
(1)若购买这两种树苗共用去26500元,则罗汉松、雪松树苗各购买多少株?
(2)绿化工程来年一般都要将死树补上新苗,现要使该两种树苗来年共补苗不多于80株,则罗汉松树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,才能使购买树苗的费用最低?请求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
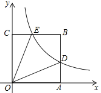
【题目】平面直角坐标系中,正方形OABC如图放置,反比例函数![]() 的图像交AB于点D,交BC于点E,已知A(
的图像交AB于点D,交BC于点E,已知A(![]() ,0),∠DOE=30°,则k的值为( )
,0),∠DOE=30°,则k的值为( )
A.![]() B.
B.![]() C.3D.3
C.3D.3![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com