
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
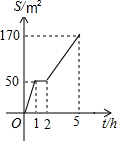 园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息后园林队每小时绿化面积为( )
园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(m2)与工作时间t(h)的函数关系的图象如图,则休息后园林队每小时绿化面积为( )| A. | 100m2 | B. | 80m2 | C. | 50m2 | D. | 40m2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直平分的四边形是正方形 | |
| B. | 16的平方根是4 | |
| C. | 两边及其一角相等的两个三角形全等 | |
| D. | 数据4,0,4,6,6的方差是4.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=180}\\{0.9x+0.85y=250}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=180}\\{0.85x+0.9y=250}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=250}\\{0.9x+0.85y=180}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=180}\\{0.85x+0.9y=250}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
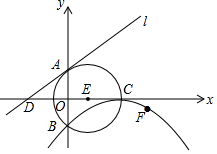 如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A,B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=$\frac{3}{4}$x+4,与x轴相交于点D.
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A,B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=$\frac{3}{4}$x+4,与x轴相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-1,3) | C. | (-2,1) | D. | (-2,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
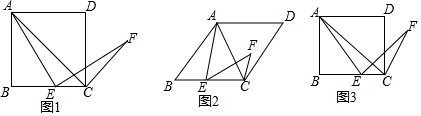
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com