
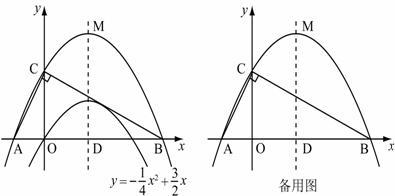
已知二次函数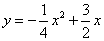 的图象如图.
的图象如图.
(1)求它的对称轴与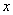 轴交点D的坐标;
轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与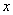 轴,
轴,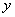 轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
 |
解: (1)由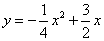 得
得 
∴D(3,0)
(2)方法一:
如图1, 设平移后的抛物线的解析式为


则C OC=
OC=
令 即
即 
得 

∴A ,B
,B
∴


∵
即: 
得 
 (舍去)
(舍去)
∴抛物线的解析式为
方法二:
∵ 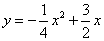
∴顶点坐标
设抛物线向上平移h个单位
则得到 ,顶点坐标
,顶点坐标
∴平移后的抛物线: 
当 时,
时, 


∴ A B
B
∵∠ACB=90° ∴△AOC∽△COB
∴ OA·OB
OA·OB

解得  ,
,
∴平移后的抛物线: 
(3)方法一:
如图2, 由抛物线的解析式 可得
可得
A(-2 ,0),B(8,0) ,C(4,0) ,M
过C、M作直线,连结CD,过M作MH垂直y轴于H
 则
则
∴

在Rt△COD中,CD= =AD
=AD
∴点C在⊙D上
∵

∴
∴△CDM是直角三角形,∴CD⊥CM
∴直线CM与⊙D相切
方法二:
如图3, 由抛物线的解析式可得
A(-2 ,0),B(8,0) ,C(4,0) ,M
作直线CM,过D作DE⊥CM于E, 过M作MH垂直y轴于H
则 ,
, 
 由勾股定理得
由勾股定理得
∵DM∥OC
∴∠MCH=∠EMD
∴Rt△CMH∽Rt△DME
∴ 得
得 
由(2)知
∴⊙D的半径为5
∴直线CM与⊙D相切


科目:初中数学 来源: 题型:
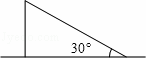
如图,一棵树在一次强台风中于离地面3米处折断倒下,倒下部分与地面成30°角,这棵树在折断前的高度为( )
A. 6米 B. 9米 C. 12米 D. 15米
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球.每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球实验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
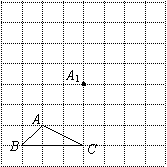
如图所示,正方形网格中,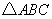 为格点三角形(即三角形的顶点都在格点上).
为格点三角形(即三角形的顶点都在格点上).
(1)把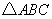 沿
沿 方向平移后,点
方向平移后,点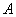 移到点
移到点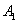 ,在网格中画出平移后得到的
,在网格中画出平移后得到的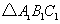 ;
;
(2)把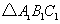 绕点
绕点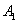 按逆时针方向旋转
按逆时针方向旋转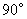 ,在网格中画出旋转后的
,在网格中画出旋转后的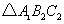 ;
;
(3)如果网格中小正方形的边长为1,求点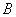 经过(1)、(2)变换的路径总长.
经过(1)、(2)变换的路径总长.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com