
【题目】已知:如图,反比例函数 ![]() 的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).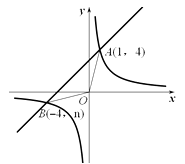
(1)求△OAB的面积;
(2)根据图象,直接写出不等式 ![]() 的解集.
的解集.
【答案】
(1)解:把A点(1,4)分别代入反比例函数 ![]() ,一次函数y=x+b,
,一次函数y=x+b,
得k=1×4,1+b=4,
解得k=4,b=3,
∴一次函数解析式是y=x+3;
如图,设直线y=x+3与y轴的交点为C,
当x=﹣4时,y=﹣1,
∴B(﹣4,﹣1),
当x=0时,y=+3,
∴C(0,3),
∴ ![]()
(2)∵B(﹣4,﹣1),A(1,4),
∴根据图象可知:当x>1或﹣4<x<0时, ![]()
【解析】(1)求出直线AB的解析式 ,求出与y轴的交点,通过分割,把△OAB的面积分成两部分,即S Δ A O B = S Δ A O C + S Δ B O C,进而求出面积;(2)利用数形结合的思想,不等式的解集转化为两图像的交点问题,即A点的左侧部分与B的右侧部分.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,A(2,0),D(6,4),将线段AD平移得到BC,B(0,﹣6),延长BC交x轴于点E.
(1)则△ABC的面积是 ;
(2)Q为x轴上一动点,当△ABC与△ADQ的面积相等时,试求点Q的坐标.
(3)若存在一点M(m,6)且△ADM的面积不小于△ABC的面积,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,FC⊥CD,∠1=∠2,∠B=60°.

(1)求∠BCF的度数;(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() 的图象开口向上,与 x轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是( )
的图象开口向上,与 x轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是( )
A.abc<0
B.b=2a
C.a+b+c=0
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13 个结,然后以3个结间距、4 个结间距、5 个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
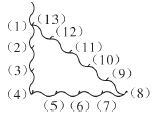
A.直角三角形两个锐角互补
B.三角形内角和等于180°
C.三角形两条短边的平方和等于长边的平方
D.如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】牛奶是最古老的天然饮料之一,被誉为“白色血液”,对人体的重要性可想而知,现已成为国家营养餐计划备选食品之一.为推行国家营养餐计划,某乳品公司向某营养餐中心运输一批牛奶,由铁路运输每千克只需运费0.58 元;由公路运输,每千克需运费0.28元,还需其他费用600元.请探究选用哪种运输方式所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点M、N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,∠A=100°,∠C=70°,则∠B= . 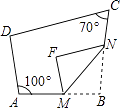
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,
①若AB=CD=1,AB//CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD.
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形.求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com