
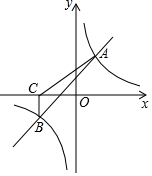
 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),分析 (1)利用待定系数法求函数的解析式;
(2)根据图象得出不等式的解集;
(3)以BC为底边,高为A、B两点的横坐标的绝对值的和,代入面积公式计算即可.
解答 解:(1)∵点A(2,3)在y=$\frac{m}{x}$的图象上,
∴m=6,
∴反比例函数的解析式为:y=$\frac{6}{x}$,
∵B(-3,n)在反比例函数图象上,
∴n=$\frac{6}{-3}$=-2,
∵A(2,3),B(-3,-2)两点在直线y=kx+b上,
∴$\left\{\begin{array}{l}{3=2k+b}\\{-2=-3k+b}\end{array}\right.$ 解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴一次函数的解析式为:y=x+1;
(2)由图象得:x<-3或0<x<2,
故答案为:x<-3或0<x<2;
(3)以BC为底边,则BC边上的高为:|-3|+2=5,
∴S△ABC=$\frac{1}{2}$×2×5=5.
点评 本题主要考查了待定系数法求反比例函数与一次函数的解析式及三角形面积的求法.这里体现了数形结合的思想,做此类题一定要正确理解坐标与图形特点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
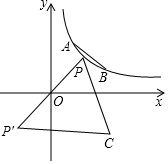 如图点A(1,2)、B(2,1)在反比例函数y=$\frac{2}{x}$图象上,点P是反比例函数y=$\frac{2}{x}$在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.
如图点A(1,2)、B(2,1)在反比例函数y=$\frac{2}{x}$图象上,点P是反比例函数y=$\frac{2}{x}$在第一象限图象上的一个动点,作点P关于原点对称的点P′,以P P′为边作等边△P P′C,点C(x,y)在第四象限.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
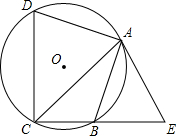 如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,AB=AC,∠A=36°.
如图所示,在△ABC中,AB=AC,∠A=36°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这组数据的众数是170 | |
| B. | 这组数据的中位数是169 | |
| C. | 这组数据的平均数是169 | |
| D. | 若从8名学生中任选1名学生参加校文艺会演,则这名学生的身高不低于170的概率为$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com