
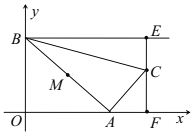
【题目】如图,点![]() 是
是![]() 轴非负半轴上的动点,点
轴非负半轴上的动点,点![]() 坐标为
坐标为![]() ,
,![]() 是线段
是线段![]() 的中点,将点
的中点,将点![]() 绕点
绕点![]() 顺时针方向旋转90°得到点
顺时针方向旋转90°得到点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,过点
,过点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
(1)当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)设![]() 的面积为
的面积为![]() ,当点
,当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)当![]() 为何值时,
为何值时,![]() 取得最小值.
取得最小值.
科目:初中数学 来源: 题型:
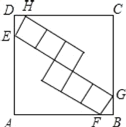
【题目】如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则每个小正方形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() 为直线
为直线![]() 上的点,
上的点,![]() 为直线
为直线![]() 上的点,分别连接
上的点,分别连接![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() ,点
,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
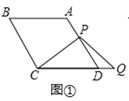
在线段![]() 的延长线上,如图①,易证:
的延长线上,如图①,易证:![]() (不需证明);
(不需证明);
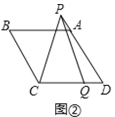
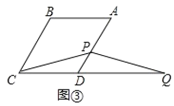
(2)如图②,若∠B=120°,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 的延长线上,如图③,猜想线段
的延长线上,如图③,猜想线段![]() ,
,![]() 和
和![]() 之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.
之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB’C’,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是___________ (结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
我们知道若一个矩形是的周长固定,当相邻两边相等,即为正方形时,它的面积最大.反过来,若一个矩形的面积固定,它的周长是否会有最值呢?
(探究方法)
用两个直角边分别为![]() ,
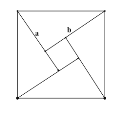
,![]() 的4个全等的直角三角形可以拼成一个正方形。若
的4个全等的直角三角形可以拼成一个正方形。若![]() ,可以拼成如图所示的正方形,从而得到
,可以拼成如图所示的正方形,从而得到![]() ,即
,即![]() ;当
;当![]() 时,中间小正方形收缩为1个点,此时正方形的面积等于4个直角三角形面积的和.即
时,中间小正方形收缩为1个点,此时正方形的面积等于4个直角三角形面积的和.即![]() .于是我们可以得到结论:
.于是我们可以得到结论:![]() ,
,![]() 为正数,总有
为正数,总有![]() ,当且仅当
,当且仅当![]() 时,代数式
时,代数式![]() 取得最小值
取得最小值![]() .另外,我们也可以通过代数式运算得到类似上面的结论:
.另外,我们也可以通过代数式运算得到类似上面的结论:
∵![]() ,∴
,∴![]() ,
,![]()
∴对于任意实数![]() ,
,![]() 总有
总有![]() ,且当
,且当![]() 时,代数式
时,代数式![]() 取最小值
取最小值![]() .
.
使得上面的方法,对于正数![]() ,
,![]() ,试比较
,试比较![]() 和
和![]() 的大小关系.
的大小关系.
(类比应用)
利用上面所得到的结论完成填空
(1)当![]() 时,代数式
时,代数式![]() 有最 值为 .
有最 值为 .
(2)当![]() 时,代数式
时,代数式![]() 有最 值为 .
有最 值为 .
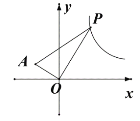
(3)如图,已知![]() 是反比例函数
是反比例函数![]() 图象上任意一动点,
图象上任意一动点,![]() ,
,![]() ,试求
,试求![]() 的最小面积.
的最小面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
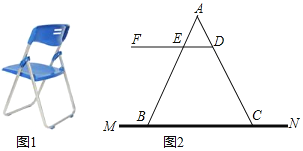
【题目】如图1是一种折叠椅,忽略其支架等的宽度,得到他的侧面简化结构图![]() 图
图![]() ,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得
,支架与坐板均用线段表示,若座板DF平行于地面MN,前支撑架AB与后支撑架AC分别与座板DF交于点E、D,现测得![]() 厘米,
厘米, ![]() 厘米,
厘米, ![]() .
.
![]() 求椅子的高度
求椅子的高度![]() 即椅子的座板DF与地面MN之间的距离
即椅子的座板DF与地面MN之间的距离![]() 精确到1厘米
精确到1厘米![]()
![]() 求椅子两脚B、C之间的距离
求椅子两脚B、C之间的距离![]() 精确到1厘米
精确到1厘米![]() 参考数据:
参考数据: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
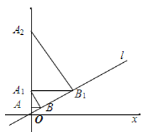
【题目】如图,已知直线l:y=![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2020的坐标为______________.
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2020的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.
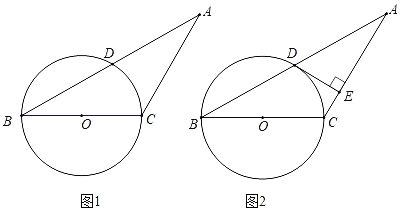
(1)求证:点D是AB的中点;
(2)如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
(1)求证:AE=DF;
(2)求证:AM⊥DF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com