
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����Ϊ��4��1���������߽�y���ڵ�A����x����B��C���㣨��B�ڵ�C����ࣩ����֪C������Ϊ��6��0����
��1����������ߵĽ���ʽ��
��2����֪��P���������ϵ�һ�����㣬��λ��A��C����֮�䣮�ʣ�����P�˶���ʲôλ��ʱ����PAC�������������PAC����������
��3������AB������B��AB�Ĵ��߽��������ڵ�D���Ե�CΪԲ�ĵ�Բ�������ߵĶԳ���l���У��Ȳ�ȫͼ�Σ����ж�ֱ��BD���C��λ�ù�ϵ������֤����
���𰸡�
��1���⣺�������ߵĶ���Ϊ��4��1����
���������߽���ʽΪy=a��x��4��2+1��
�������߾�����C��6��0����
��0=a��6��4��2+1�����a=�� ![]() ��
��
��y=�� ![]() ��x��4��2+1=��
��x��4��2+1=�� ![]() x2+2x��3��
x2+2x��3��
���������ߵĽ���ʽΪy=�� ![]() x2+2x��3��
x2+2x��3��
��2���⣺��ͼ1������P��ƽ����y���ֱ�߽�AC�ڵ�Q��

��A��0����3����C��6��0����
��ֱ��AC����ʽΪy= ![]() x��3��
x��3��
��P��������m���� ![]() m2+2m��3����
m2+2m��3����
��Q���������m�� ![]() m��3����
m��3����
��PQ=�� ![]() m2+2m��3����
m2+2m��3���� ![]() m��3��=��
m��3��=�� ![]() m2+
m2+ ![]() m��
m��
��S��PAC=S��PAQ+S��PCQ= ![]() ������
������ ![]() m2+
m2+ ![]() m����6=��
m����6=�� ![]() ��m��3��2+
��m��3��2+ ![]() ��
��
�൱m=3ʱ����PAC��������Ϊ ![]() ��
��
�ߵ�m=3ʱ���� ![]() m2+2m��3=
m2+2m��3= ![]() ��
��
��P��������3�� ![]() ����
����
���ϣ�P���λ���ǣ�3�� ![]() ������PAC����������
������PAC���������� ![]() ��
��
��3���⣺�ж�ֱ��BD���C���룮
֤����� ![]() ��x��4��2+1=0�����x1=2��x2=6��
��x��4��2+1=0�����x1=2��x2=6��
��B�����꣨2��0����
�֡������߽�y���ڵ�A��
��A��������0����3����
��AB= ![]() ��
��
���C��Գ���l�����ڵ�F�����C�İ뾶CF=2��
��CE��BD�ڵ�E����ͼ2�����BEC=��AOB=90�㣮

�ߡ�ABD=90�㣬
���CBE=90�㩁��ABO��
�֡ߡ�BAO=90�㩁��ABO��
���BAO=��CBE��
���AOB�ס�BEC��
�� ![]() ��
��
�� ![]() ��
��
��CE= ![]() ��2��
��2��
��ֱ��BD���C���룮
����������1�����ڱ�������������ߵĶ��㣬���趥��ʽ��Ȼ���ְѵ�C��������뼴�����������ϵ��a��ֵ���Ӷ��ó���������ʽ��
��2����ͼ1������P��ƽ����y���ֱ�߽�AC�ڵ�Q����A,C��������꣬���ô���ϵ�������ֱ��AC�Ľ���ʽ�������������ϵ�������ص����P������꣬������ʾ��Q������꣬�Ӷ���ʾ��PQ�ij��ȣ�����S��PAC=S��PAQ+S��PCQ��������������ϵʽ������Ϊ����ʽ֪��m=3ʱ����PAC��������Ȼ���m=3����P����������ʽ���Ӷ��ó�P������ꣻ
��3���ж�ֱ��BD���C���룮�����ҵ�B��A������꣬���ݹ��ɶ����ó�AB�ij������C��Գ���l�����ڵ�F�����C�İ뾶CF=2����CE��BD�ڵ�E����ͼ2�����BEC=��AOB=90�㣬Ȼ�����ͬ�ǵ������ȵó���BAO=��CBE�������жϳ���AOB�ס�BEC���������������ε����ʵ����ʵó�CE�ij��Ӷ�����ֱ����Բ��λ�ù�ϵ�����жϼ��ɡ�
�����㾫�����������������ε��ж��������ǽ����ĸ�������Ҫ֪�����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㲹ȫ֤�����̣���ͼ��DG��BC��AC��BC��EF��AB����1=��2����֤��EF��CD

֤������DG��BC��AC��BC(��֪)
���DGB=90�㣬��ACB=90��٣� ��
���DGB=��ACB ��( )
��DG��AC ��( )
���2= ��________ �ݣ� ��
�֡�1=��2 �ޣ� ��
���1=��DCA �ߣ� ��
��EF��CD �ࣨ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�AD=CD����DAB=��ACB=90�㣬����D��DE��AC������ΪF�� 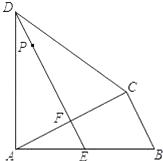
DE��AB�ཻ�ڵ�E��
��1����֤��ABAF=CBCD��
��2����֪AB=15cm��BC=9cm��P���߶�DE�ϵĶ��㣮��DP=x cm������BCDP�����Ϊy ![]() ��
��
����y����x�ĺ�����ϵʽ��
��y�Ƿ�������ֵ���������������ֵ������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ھ���ABCD�У�BC��8��CD��6������BCD�ضԽ���BD���ۣ���C���ڵ�C������BC����AD�ڵ�E������BDE�����Ϊ��������
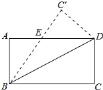
A. ![]() B.
B. ![]() C. 21D. 24
C. 21D. 24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l���O��AB�ǡ�O��ֱ����AD��l�ڵ�D��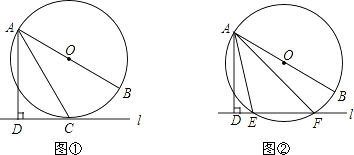
��1����ͼ�٣���ֱ��l���O�����ڵ�Cʱ����֤��ACƽ�֡�DAB��
��2����ͼ�ڣ���ֱ��l���O�ཻ�ڵ�E��Fʱ����֤����DAE=��BAF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
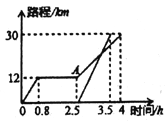
����Ŀ����ĩ��С���������������������棬���Ӽҳ���0.8Сʱ��ﵽ������ǣ�����һ��ʱ������������������������С�����һ��ʱ��ְּݳ�����ͬ��·��ǰ��������. ��ͼ���������·��s��km����С�����ʱ��t��h���Ĺ�ϵͼ�������ͼ�ش��������⣺
��1��ͼ���Ա�����____���������______��
��2��С���ҵ���������·��Ϊ____ km��С����������Ƕ�����ʱ��Ϊ____ h��
��3��С������______Сʱ��ְּݳ�������
��4��ͼ��A���ʾ___________________________________��
��5��С����������ǵ���������ƽ���ٶ�Ϊ______km/h��С���ְּݳ���ƽ���ٶ�Ϊ______km/h�������䣻�ְּݳ�����______��С������
��6��С���Ӽҵ��������ʱ�������·��s������ʱ��t֮��Ĺ�ϵʽΪ________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶OD����AB�ڵ�C������AO���ӳ�����O�ڵ�E������EC����AB=8��CD=2����EC�ij�Ϊ�� ��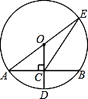
A.2 ![]()
B.2 ![]()
C.2 ![]()
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱߡ�ABC�Ķ���A��C������һֻ��ţ������ͬʱ�������ֱ���ÿ����1���ٶ���A��B����C��A���У�����һֻ��ţ�����յ�ʱ����һֻҲֹͣ�˶�������t���Ӻ����Ƿֱ����е�D��E�������ʣ�
��1����ͼ1�������й����У�CD��BEʼ���������֤����
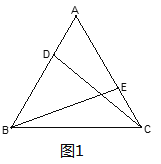
��2�������ԭ���еġ���A��B����C��A���С�����Ϊ������AB��CA���ӳ������С���EB��CD���ڵ�Q�������������䣬��ţ���й����С�CQE�Ĵ�С���ֲ��䣬������ͼ2˵������CQE=60�㣻
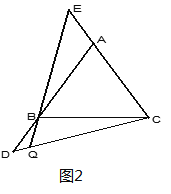
��3�������ԭ���С���C��A���С���Ϊ������BC���ӳ������У�����DE��AC��F���������������䣬��ͼ3�������й����У�֤����DF=EF
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����һ�ֽ���Ϊ20 ��Ԫ/�����ļ���������������y ������������ۼ۸�x ��Ԫ/����֮��Ϊһ�κ�����ϵ����仯���±���
�۸�x ��Ԫ/���� | �� | 30 | 50 | �� |
������y ������� | �� | 5 | 3 | �� |
ͬʱ�����۹����е�������֧���������ۣ��ܼ�40��Ԫ�����ù�˾Ҫ���40��Ԫ�ľ������Ҿ������ù˿͵õ�ʵ�ݣ���ô���ۼ۸�Ӧ��Ϊ���٣�
��ע��������=�����۶�ܽ��۩�������֧��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com