

分析 (1)用“经常参加”所占的百分比乘以360°计算即可得解;
(2)先求出“经常参加”的人数,然后求出喜欢篮球的人数,再补全统计图即可;
(3)根据喜欢乒乓球的27人都是“经常参加”的学生,“偶尔参加”的学生中也会有喜欢乒乓球的考虑解答;
(4)求得从不参加的总人数,根据概率公式求解可得.
解答 解:(l)“经常参加”所对应的圆心角的度数为360°×(1-15%-45%)=144°,
故答案为:144°;
(2)经常参加的人数为300×(1-15%-45%)=120人,
则“篮球”选项的人数为120-(27+33+20)=40.
补全条形统计图如下: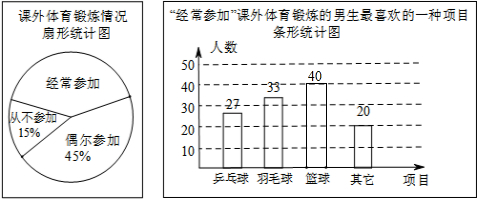
(3)这种说法不正确.
理由如下:最喜欢兵乓球的人在“经常参加”课外活动的人中有27人,而在“偶尔参加”课外活动的人中也有可能有人喜欢兵乓球,
因此比例不一定是$\frac{27}{300}$,
因此这种说法是错误的.
(4)∵从不参加的总人数为300×15%=45(人),
∴P(小王)=$\frac{10}{45}$=$\frac{2}{9}$.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
如图,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
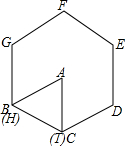 正△ABC与正六边形DEFGH的边长相等,初始如图所示,将三角形绕点I顺时针旋转使得AC与CD重合,再将三角形绕点D顺时针旋转使得AB与DE重合,…,按这样的方式将△ABC旋转2015次后,△ABC中与正六边形DEFGHI重合的边是( )
正△ABC与正六边形DEFGH的边长相等,初始如图所示,将三角形绕点I顺时针旋转使得AC与CD重合,再将三角形绕点D顺时针旋转使得AB与DE重合,…,按这样的方式将△ABC旋转2015次后,△ABC中与正六边形DEFGHI重合的边是( )| A. | AB | B. | BC | C. | AC | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
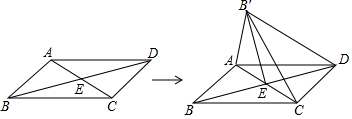
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com