
【题目】如图,抛物线y=﹣![]() x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).
x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,并证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.
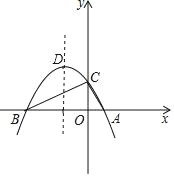
【答案】(1)顶点D的坐标为(﹣![]() ,
,![]() );(2)△ABC是直角三角形(3)当M的坐标为(﹣
);(2)△ABC是直角三角形(3)当M的坐标为(﹣![]() ,
,![]() )
)
【解析】分析:(1)、将点A的坐标代入函数解析式求出b的值,然后将二次函数进行配方从而得出顶点坐标;(2)、根据二次函数的解析式分别得出点A、B、C的坐标,然后分别求出AC、BC和AB的长度,然后根据勾股定理的逆定理得出答案;(3)、由抛物线的性质可知,点A与点B关于对称轴对称,则BC与对称轴的交点就是点M,根据一次函数的交点求法得出点M的坐标.
详解:(1)、∵点A(1,0)在抛物线y=﹣![]() x2+bx+2上,∴﹣
x2+bx+2上,∴﹣![]() +b+2=0,解得,b=﹣
+b+2=0,解得,b=﹣![]() ,
,
抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+2,y=﹣
x+2,y=﹣![]() x2﹣
x2﹣![]() x+2=﹣
x+2=﹣![]() (x+
(x+![]() )2+
)2+![]() ,
,
则顶点D的坐标为(﹣![]() ,
,![]() );
);
(2)、△ABC是直角三角形,
证明:点C的坐标为(0,2),即OC=2, ﹣![]() x2﹣
x2﹣![]() x+2=0, 解得,x1=﹣4,x2=1,
x+2=0, 解得,x1=﹣4,x2=1,
则点B的坐标为(﹣4,0),即OB=4,OA=1,OB=4, ∴AB=5,
由勾股定理得,AC=![]() ,BC=2
,BC=2![]() , AC2+BC2=25=AB2, ∴△ABC是直角三角形;
, AC2+BC2=25=AB2, ∴△ABC是直角三角形;
(3)、由抛物线的性质可知,点A与点B关于对称轴对称,
连接BC交对称轴于M,此时△ACM的周长最小, 设直线BC的解析式为:y=kx+b,
由题意得,![]() , 解得,
, 解得,![]() , 则直线BC的解析式为:y=
, 则直线BC的解析式为:y=![]() x+2,
x+2,
当x=﹣![]() 时,y=
时,y=![]() , ∴当M的坐标为(﹣
, ∴当M的坐标为(﹣![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
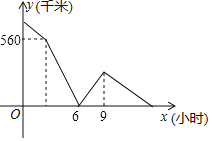
【题目】A、B、C三地在同一直线上,甲、乙两车分别从A,B两地相向匀速行驶,甲车先出发2小时,甲车到达B地后立即调头,并将速度提高10%后与乙车同向行驶,乙车到达A地后,继续保持原速向远离B的方向行驶,经过一段时间后两车同时到达C地,设两车之间的距离为y(千米),甲行驶的时间x(小时).y与x的关系如图所示,则B、C两地相距_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是![]() 的角平分线OC上一点,PN
的角平分线OC上一点,PN![]() OB于点N,点M是线段ON上一点,已知OM=3,ON=4,点D为OA上一点,若满足PD=PM,则OD的长度为________
OB于点N,点M是线段ON上一点,已知OM=3,ON=4,点D为OA上一点,若满足PD=PM,则OD的长度为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以![]() cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA-AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),求在这一运动过程中y与x之间函数关系式.
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA-AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),求在这一运动过程中y与x之间函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中![]() ,
,![]() ,詹姆斯在探究筝形的性质时,得到如下结论:
,詹姆斯在探究筝形的性质时,得到如下结论:![]() ;
;![]() ;
;![]() ≌
≌![]() ;
;![]() 四边形ABCD的面积
四边形ABCD的面积![]() 其中正确的结论有
其中正确的结论有![]()
![]()

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贵州省是我国首个大数据综合试验区,大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值,为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:

(1)本次参与调查的人数有 人;
(2)关注城市医疗信息的有 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是 度;
(4)说一条你从统计图中获取的信息.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,弦BC的长为![]() ,点A为弦BC所对优弧上任意一点(B,C两点除外).
,点A为弦BC所对优弧上任意一点(B,C两点除外).
 (1)求∠BAC的度数;
(1)求∠BAC的度数;
(2)求△ABC面积的最大值.
(参考数据:![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com