
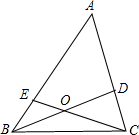
 如图,三角形ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE.若△BOC的面积=2,则四边形AEOD的面积等于( )
如图,三角形ABC内的线段BD、CE相交于点O,已知OB=OD,OC=2OE.若△BOC的面积=2,则四边形AEOD的面积等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 连接AO,利用等高不等底的三角形面积比等于底长的比,可求出△COD与△BOE的面积.列出关于△AOE与△AOD的面积的方程即可求出四边形AEOD的面积.
解答 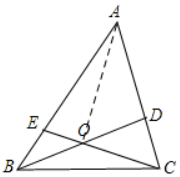 解:连接OA,
解:连接OA,
∵OB=OD,
∴S△BOC=S△COD=2,
∵OC=2OE,
∴S△BOE=$\frac{1}{2}$S△BOC=1,
∵OB=OD,
∴S△AOB=S△AOD,
∴S△BOE+S△AOE=S△AOD,
即:1+S△AOE=S△AOD①,
∵OC=2OE,
∴S△AOC=2S△AOE,
∴S△AOD+S△COD=2S△AOE,
即:S△AOD+2=2S△AOE②,
联立①和②:解得:S△AOE=3,S△AOD=4,
S四边形AEOD=S△AOE+S△AOD=7,
故选(D)
点评 本题考查三角形面积问题,涉及方程组的解法,注意灵活运用等高不等底的三角形面积比等于底长的比这一结论.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
| A. | 1.25×109 | B. | 0.125×1010 | C. | 12.5×108 | D. | 1.25×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
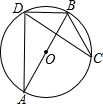 如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )
如图,D、C是⊙O上的两点,AB经过圆心O,若∠C=30°,AD=3,则⊙O的直径为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
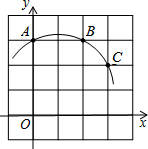 如图,在带有正方形网格的平面直角坐标系xOy中,一条圆弧经过A(0,3),B(2,3),C(3,2)三点,那么这条圆弧所在圆的圆心坐标是( )
如图,在带有正方形网格的平面直角坐标系xOy中,一条圆弧经过A(0,3),B(2,3),C(3,2)三点,那么这条圆弧所在圆的圆心坐标是( )| A. | (0,0) | B. | (1,1) | C. | (0,1) | D. | (1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
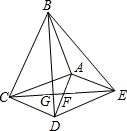 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连结CE交AD于点F,连结BD交CE于点G,连结BE.下列结论中,正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连结CE交AD于点F,连结BD交CE于点G,连结BE.下列结论中,正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com