
【题目】在平面直角坐标系中,o为坐标原点,点A的坐标为(![]() ,3),点B的坐标(
,3),点B的坐标(![]() ,6).
,6).
(1)若AB与坐标轴平行,求AB的长;
(2)若![]() 满足
满足![]() AC⊥
AC⊥![]() 轴,垂足为C,BD⊥
轴,垂足为C,BD⊥![]() 轴,垂足为D:
轴,垂足为D:
①求四边形ACDB的面积;
②连AB、OA、OB,若△OAB的面积大于6而小于10,求![]() 的取值范围。
的取值范围。
【答案】(1)AB=3;(2)①9;②6<a<![]() 或﹣
或﹣![]() <a<﹣2
<a<﹣2
【解析】
(1)分析题意可知,AB与y轴平行,则AB的长为两点的纵坐标之差;
(2)①先解方程组得到b﹣a=2,则根据梯形的面积公式可计算出四边形ACDB的面积为9;
②分类讨论:当a>0,S△OAB=S△OBD﹣S△OAC﹣S梯形ACDB=![]() a﹣3,则6<
a﹣3,则6<![]() a﹣3<10,解得6<a<
a﹣3<10,解得6<a<![]() ;当a<0,b>0,S△OAB=S梯形ACDB﹣S△OBD﹣S△OAC=3﹣
;当a<0,b>0,S△OAB=S梯形ACDB﹣S△OBD﹣S△OAC=3﹣![]() a,则6<3﹣
a,则6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,而b=2+a>0,则a>﹣2,故舍去;当a<0,b<0,S△OAB=S△OBD+S梯形ACDB﹣S△OAC=3﹣
<a<﹣2,而b=2+a>0,则a>﹣2,故舍去;当a<0,b<0,S△OAB=S△OBD+S梯形ACDB﹣S△OAC=3﹣![]() a,则6<3﹣
a,则6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,于是得到a的取值范围为6<a<
<a<﹣2,于是得到a的取值范围为6<a<![]() 或﹣
或﹣![]() <a<﹣2.
<a<﹣2.
(1)∵AB与坐标轴平行,即AB平行于y轴,
∴AB=6﹣3=3;
(2)①由方程组![]() 得b﹣a=2,
得b﹣a=2,
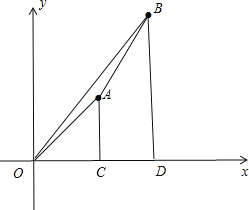
∵AC⊥x轴,垂足为C,BD⊥x轴,垂足为D,
∴C(a,0),D(b,0),如图,
∴四边形ACDB的面积=![]() (3+6)(b﹣a)=
(3+6)(b﹣a)=![]() 92=9;
92=9;
②当a>0,
∵S△OAB=S△OBD﹣S△OAC﹣S梯形ACDB,
∴S△OAB=![]() 6b﹣
6b﹣![]() 3a﹣9=3b﹣
3a﹣9=3b﹣![]() a﹣9,
a﹣9,
而b=2+a,
∴S△OAB=3(2+a)﹣![]() a﹣9=
a﹣9=![]() a﹣3,
a﹣3,
∴6<![]() a﹣3<10,解得6<a<
a﹣3<10,解得6<a<![]() ;
;
当a<0,b>0,
S△OAB=S梯形ACDB﹣S△OBD﹣S△OAC=9﹣![]() 6b+
6b+![]() 3a=9﹣3b+
3a=9﹣3b+![]() a=9﹣3(2+a)+
a=9﹣3(2+a)+![]() a=3﹣
a=3﹣![]() a
a
∴6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,
<a<﹣2,
而b=2+a>0,则a>﹣2,故舍去,
当a<0,b<0,
∵S△OAB=S△OBD+S梯形ACDB﹣S△OAC=﹣![]() 6b+9+
6b+9+![]() 3a=﹣3b+9+
3a=﹣3b+9+![]() a=﹣3(2+a)+9+
a=﹣3(2+a)+9+![]() a=3﹣
a=3﹣![]() a
a
∴6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,
<a<﹣2,
综上所述,a的取值范围为6<a<![]() 或﹣
或﹣![]() <a<﹣2.
<a<﹣2.


科目:初中数学 来源: 题型:
【题目】(7分)为倡导节约用电,某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)(4分)小张家2015年2月份用电100千瓦时,上缴电费68元;3月份用电120千瓦时,上缴电费88元.问“基本电价”和“提高电价”分别为多少元/千瓦时?
(2)(3分)若4月份小张家预计用电130千瓦时,请预算小张家4月份应上缴的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“单词的记忆效率“是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.如图描述了某次单词复习中小华,小红小刚和小强四位同学的单词记忆效率y与复习的单词个数x的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )

A. 小华B. 小红C. 小刚D. 小强
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?遇到这样的问题,我们可以先思考一下,从简单的情形入手.先分别计算下列各式的值:
①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
…
由此我们可以得到:(x﹣1)(x99+x98+x97+…+x+1)= .
请你利用上面的结论,再完成下面两题的计算:
(1)210+29+28+…+2+1
(2)3n+3n-1+3n-2…+3+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:图象①②③均是以P0为圆心,1个单位长度为半径的扇形,将图形①②③分别沿东北,正南,西北方向同时平移,每次移动一个单位长度,第一次移动后图形①②③的圆心依次为P1P2P3,第二次移动后图形①②③的圆心依次为P4P5P6…,依此规律,P0P2018=_____个单位长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为 ![]() cm,AC=8cm,设运动时间为t秒.
cm,AC=8cm,设运动时间为t秒. 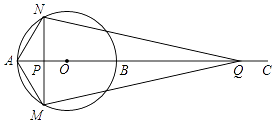
(1)求证:NQ=MQ;
(2)填空: ①当t=时,四边形AMQN为菱形;
②当t=时,NQ与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com