
 二次函数y=$\frac{2}{3}{x^2}$的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A100在y
二次函数y=$\frac{2}{3}{x^2}$的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A100在y分析 分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,设A0A1=a,A1A2=b,A2A3=c,则AB1=$\frac{\sqrt{3}}{2}$a,BB2=$\frac{\sqrt{3}}{2}$b,CB3=$\frac{\sqrt{3}}{2}$c,再根据所求正三角形的边长,分别表示B1,B2,B3的纵坐标,逐步代入抛物线y=$\frac{2}{3}$x2中,求a、b、c的值,得出规律.
解答 解:分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,
设A0A1=a,A1A2=b,A2A3=c,则AB1=$\frac{\sqrt{3}}{2}$a,BB2=$\frac{\sqrt{3}}{2}$b,CB3=$\frac{\sqrt{3}}{2}$c,
在正△A0B1A1中,B1($\frac{\sqrt{3}}{2}$a,$\frac{a}{2}$),
代入y=$\frac{2}{3}$x2中,得$\frac{a}{2}$=$\frac{2}{3}$•($\frac{\sqrt{3}}{2}$a)2,解得a=1,
∴B1($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),
在正△A1B2A2中,B2($\frac{\sqrt{3}}{2}$b,1+$\frac{b}{2}$),
代入y=$\frac{2}{3}$x2中,得1+$\frac{b}{2}$=$\frac{2}{3}$•($\frac{\sqrt{3}}{2}$b)2,解得b=2,
∴B2($\sqrt{3}$,2),
在正△A2B3A3中,B3($\frac{\sqrt{3}}{2}$c,3+$\frac{c}{2}$),
代入y=$\frac{2}{3}$x2中,得3+$\frac{c}{2}$=$\frac{2}{3}$•($\frac{\sqrt{3}}{2}$c)2,解得c=3,
∴B3($\frac{3\sqrt{3}}{2}$,$\frac{9}{2}$),
…,
由此可得B100的坐标为$({50\sqrt{3},5000})$.
故答案为$({50\sqrt{3},5000})$.
点评 本题考查了二次函数的综合运用.关键是根据正三角形的性质表示点的坐标,利用抛物线解析式求正三角形的边长,得到规律.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
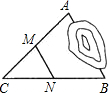 如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )| A. | AB=12m | B. | MN∥AB | C. | △CMN∽△CAB | D. | CM:MA=1:2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 次数 | 一 | 二 | 三 | 四 | 五 |
| 水位(厘米) | 13 | 5 | -0.5 | -3 | -15 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a,b,c为常数a≠0)的图象如图所示,下列结论正确的是( )
已知二次函数y=ax2+bx+c(a,b,c为常数a≠0)的图象如图所示,下列结论正确的是( )| A. | 2a+b<0 | B. | 4a+2b+c>0 | ||
| C. | m(am+b)>a+b(m为大于1的实数) | D. | 3a+c<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com