Question

6．直线MN与PQ相互垂直，垂足为点O，点A在射线OQ上运功，点B在射线OM上运动，点A、点B均不与点O重合．
（1）如图①，AI平分∠BAO，BI平分∠ABO，若∠BAO=40°，求∠AIB的度数．
（2）如图②，AI平分∠BAO，BC平分∠ABM，BC的反向延长线交AI于点D．
①若∠BAO=40°，则∠ADB=45°度（直接写出结果，不需说理）
②点A、B在运动的过程中，若∠BAO=m°，试求∠ADB的度数．
（3）如图③，已知点E在BA的延长线上，∠BAO的角平分线AI、∠OAE的角平分线AF与∠BOP的角平分线所在的直线分别相交于点D、F，在△ADF中，如果有一个角的度数是另一个角的4倍，请直接写出∠ABO的度数．

Answer 1

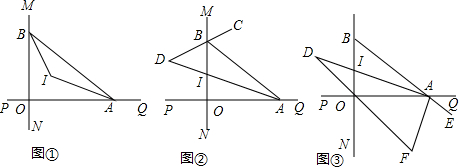
分析 （1）求出∠IBA，∠IAB，根据∠AIB=180°-（∠IBA+∠IAB），即可解决问题．
（2）①根据∠CBA=∠D+∠BAD，只要求出∠CBA，∠BAD即可．
②结论：点A、B在运动的过程中，∠ADB=45°．根据∠D=∠CBA-∠BAD=$\frac{1}{2}$∠MBA-$\frac{1}{2}$∠BAO=$\frac{1}{2}$（∠MBA-∠BAO）=$\frac{1}{2}$∠AOB计算即可．
（3）首先证明∠ABO=2∠D，∠DAF=90°，再分四种情形讨论即可①当∠DAF=4∠D时，②当∠DAF=4∠F时，③当∠F=4∠D时，④当∠D=4∠F时，分别计算即可．

解答 解：（1）如图①中，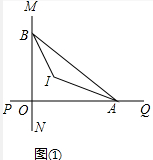

∵MN⊥PQ，
∴∠AOB=90°，∵∠OAB=40°，
∴∠ABO=90°-∠OAB=50°，
∵AI平分∠BAO，BI平分∠ABO，
∴∠IBA=$\frac{1}{2}$ABO=25°，∠IAB=$\frac{1}{2}$∠OAB=20°，
∴∠AIB=180°-（∠IBA+∠IAB）=135°．
（2）如图②中，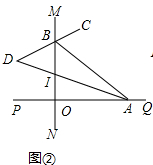

①∵∠MBA=∠AOB+∠BAO=90°+40°=130°，
∵AI平分∠BAO，BC平分∠ABM，
∴∠CBA=$\frac{1}{2}$∠MBA=65°，∠BAI=$\frac{1}{2}$∠BAO=20°，
∵∠CBA=∠D+∠BAD，
∴∠D=45°．
②结论：点A、B在运动的过程中，∠ADB=45°
理由：∵∠D=∠CBA-∠BAD=$\frac{1}{2}$∠MBA-$\frac{1}{2}$∠BAO=$\frac{1}{2}$（∠MBA-∠BAO）=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×90°=45°，
∴点A、B在运动的过程中，∠ADB=45°．

（3）如图③中，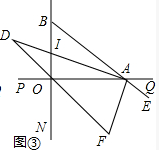

∵∠BAO的角平分线AI、∠OAE的角平分线AF与∠BOP的角平分线所在的直线分别相交于点D、F，
∴∠DAO=$\frac{1}{2}$∠BAO，∠FAO=$\frac{1}{2}$∠EAP，
∴∠DAF=$\frac{1}{2}$∠BAO+$\frac{1}{2}∠EAP$=$\frac{1}{2}$×180°=90°，
∴∠D=∠POD-∠DAO=$\frac{1}{2}$∠POB-$\frac{1}{2}$∠BAO=$\frac{1}{2}$（∠POB-∠BAO）=$\frac{1}{2}$∠ABO，
①当∠DAF=4∠D时，∠D=22.5°，
∴∠ABO=2∠D=45°．
②当∠DAF=4∠F时，∠F=22.5°，∠D=67.5°，
∴∠B=2∠D=135°（不合题意舍弃）．
③当∠F=4∠D时，∠D=18°，
∴∠ABO=2∠D=36°．
④当∠D=4∠F时，∠D=72°，
∴∠ABP=2∠D=144°（不合题意舍弃）．
综上所述，当∠ABO=45°或36°时，在△ADF中，有一个角的度数是另一个角的4倍．

点评 本题考查三角形综合题、三角形内角和定理、角平分线的定义、三角形的外角等知识，解题的关键是灵活运用这些知识解决问题，学会分类讨论的思想思考问题，属于中考常考题型．