
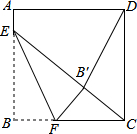
 如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为16或4$\sqrt{5}$.
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为16或4$\sqrt{5}$. 分析 根据翻折的性质,可得B′E的长,根据勾股定理,可得CE的长,根据等腰三角形的判定,可得答案.
解答 解:(i)如图1所示:当B′D=B′C时,过B′点作GH∥AD,则∠B′GE=90°.
当B′C=B′D时,AG=DH=$\frac{1}{2}$DC=8.
由AE=3,AB=16,得BE=13.
由翻折的性质,得B′E=BE=13.
∴EG=AG-AE=8-3=5,
∴B′G=$\sqrt{B′{E}^{2}-E{G}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∴B′H=GH-B′G=16-12=4,
∴DB′=$\sqrt{B′{H}^{2}+D{H}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$
(ii)当DB′=CD时,则DB′=16(易知点F在BC上且不与点C、B重合).
(iii)如图2所示:
当CB′=CD时,
∵EB=EB′,CB=CB′,
∴点E、C在BB′的垂直平分线上,
∴EC垂直平分BB′,
由折叠可知点F与点C重合,不符合题意,舍去.
综上所述,DB′的长为16或4$\sqrt{5}$.
故答案为:16或4$\sqrt{5}$.
点评 本题考查了翻折变换、勾股定理、等腰三角形的判定,分类讨论是解题的关键.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:解答题
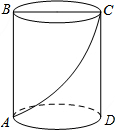 如图,一圆柱体的底面周长为24cm,高AB为16cm,BC是上底面的直径.一只昆虫从点A出发,沿着圆柱的侧面爬行到点C,求昆虫爬行的最短路程.
如图,一圆柱体的底面周长为24cm,高AB为16cm,BC是上底面的直径.一只昆虫从点A出发,沿着圆柱的侧面爬行到点C,求昆虫爬行的最短路程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 球的截面一定是圆 | |
| B. | 组成长方体的各个面中不可能有正方形 | |
| C. | 从三个不同的方向看正方体,得到的都是正方形 | |
| D. | 圆锥的截面可能是圆 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{2x-y=7}\\{3y=2x-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=1}\\{xy=12}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{\frac{y}{3}-\frac{x}{2}-1}\\{2{x}^{2}+3y-15}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{x}-\frac{2}{y}=1}\\{x+y=10}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com