����⣺��1���ߵ�C��ֱ��AB��y=-2x+42�ϣ���C��ĺ�����Ϊ16��
��y=-2��16+42=10������C��������Ϊ10��
��D����ֱ��OB��y=x�ϣ���D��ĺ�����Ϊ4��
���D��������Ϊ4��
��2���ɣ�1��֪��C������Ϊ��16��10������D������Ϊ��4��4����
��������y=ax
2-2x+c����C��D���㣬
��
��
��ã�
��
�������ߵĽ���ʽΪy=
x
2-2x+10��
��3����QΪ�߶�OB��һ�㣬������Ϊ5��
��Q��ĺ�����ҲΪ5��
�ߵ�P���������ϣ�������Ϊ5��
��
x
2-2x+10=5��
���x
1=8+2
��x
2=8-2
��
����P��������8+2
��5������Q������Ϊ��5��5�����߶�PQ�ij�Ϊ2
+3��
����P��������8-2
��5������Q������Ϊ��5��5�����߶�PQ�ij�Ϊ2
-3��
�����߶�PQ�ij�Ϊ2
+3��2
-3��
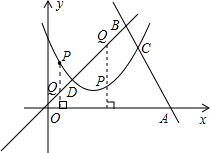
��4����PQ��x�ᣬ
��P��Q����ĺ�������ͬ����Ϊm��
��P��m��
m
2-2m+10����Q��m��m������ʱQ���߶�OB�ϣ���Q��m��-2m+42������ʱQ���߶�AB�ϣ���
��
��
���
��
���B��������14��14����
�ٵ���QΪ�߶�OB��ʱ����ͼ��ʾ��
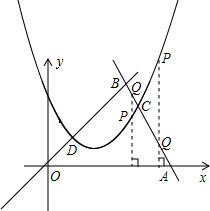
��OD�Σ�����0��m��4ʱ��d=��
m
2-2m+10��-m=
m
2-3m+10=
��m-12��
2-8��d��m�����������
��BD�Σ�����4��m��14ʱ��d=m-��
m
2-2m+10��=-
m
2+3m-10=-
��m-12��
2+8��
�ڶԳ����Ҳ࣬d��m���������С������12��m��14ʱ��d��m���������С��
��0��m��4��12��m��14ʱ��d��m���������С��
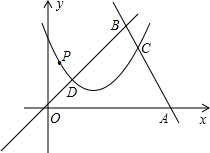
�ڵ���QΪ�߶�AB��ʱ����ͼ��ʾ��
��BC�Σ�����14��m��16ʱ��d=��-2m+42��-��
m
2-2m+10��=-
m
2+32��
�ڶԳ����Ҳ࣬d��m���������С������14��m��16ʱ��d��m���������С��
��CA�Σ�����16��m��21ʱ��d=��
m
2-2m+10��-��-2m+42��=
m
2-32��
�ڶԳ�����࣬d��m���������С��m������������
������������0��m��4��12��m��16ʱ��d��m���������С��

 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-2x+42��x�����A����ֱ��y=x�ڵ�B��������y=ax2-2x+c�ֱ��߶�AB��OB�ڵ�C��D����C�͵�D�ĺ�����ֱ�Ϊ16��4����P�������������ϣ�
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-2x+42��x�����A����ֱ��y=x�ڵ�B��������y=ax2-2x+c�ֱ��߶�AB��OB�ڵ�C��D����C�͵�D�ĺ�����ֱ�Ϊ16��4����P�������������ϣ� ��4����PQ��x�ᣬ
��4����PQ��x�ᣬ ��OD�Σ�����0��m��4ʱ��d=��
��OD�Σ�����0��m��4ʱ��d=��

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD�� ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ����� ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y= ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��