
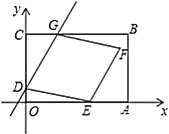
【题目】如图,平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 的直线与矩形
的直线与矩形![]() 的边
的边![]() 交于点
交于点![]() ,且点
,且点![]() 不与点
不与点![]() 重合.以
重合.以![]() 为一边作菱形
为一边作菱形![]() ,点
,点![]() 在矩形
在矩形![]() 的边
的边![]() 上,设直线
上,设直线![]() 的函数表达式为
的函数表达式为![]() .
.
(1)当![]() 时,求直线
时,求直线![]() 的函数表达式;
的函数表达式;
(2)当点![]() 的坐标为
的坐标为![]() 时,求直线
时,求直线![]() 的函数表达式;
的函数表达式;
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的长为
的长为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的函数表达式及自变量
的函数表达式及自变量![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
![]() .
.
【解析】
(1)利用矩形的性质结合点B的坐标可得出点A,C的坐标,由点D的坐标结合CG=OD可得出点G的坐标,由点D,G的坐标,利用待定系数法即可求出直线DG的函数表达式;
(2)利用勾股定理可求出DE的长,由菱形的性质及勾股定理可求出CG的长,进而可得出点G的坐标,由点D,G的坐标,利用待定系数法即可求出直线DG的函数表达式;
(3)设DG交x轴于点P,过点F作FM⊥x轴于点M,延长MF交BC于点N,易证△DCG≌△FME(AAS),利用全等三角形的性质可得出FM的长度,进而可得出FN的长,再利用三角形的面积公式可得出S与a的函数表达式,结合点G不与点C重合及点E在OA上可求出a的取值范围,此题得解.
解:(1)∵四边形OABC为矩形,点B的坐标为(7,5),点A,C分别在x轴,y轴上,
∴点C的坐标为(0,5),点A的坐标为(7,0).
∵点D的坐标为(0,1),CG=OD,
∴点G的坐标为(1,5).
将D(0,1),G(1,5)代入y=kx+b,得:
![]() ,解得
,解得![]() ,
,
∴当CG=OD时,直线DG的函数表达式为y=4x+1.
(2)在Rt△ODE中,OD=1,OE=5,∠DOE=90°
∴DE=![]() ,
,
∵四边形DEFG为菱形,
∴DG=DE=![]() .
.
在Rt△CDG中,DG=![]() ,CD=OC-OD=4,∠DCG=90°,
,CD=OC-OD=4,∠DCG=90°,
∴CG=![]()
∴点G的坐标为(![]() ,5).
,5).
将D(0,1),G(![]() ,5)代入y=kx+b,得:
,5)代入y=kx+b,得:
 ,解得:
,解得: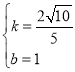
∴当CG=OD时,直线DG的函数表达式为y=![]()
(3)设DG交x轴于点P,过点F作FM⊥x轴于点M,延长MF交BC于点N,如图所示.
∵DG∥EF,
∴∠FEM=∠GPO.
∵BC∥OA,
∴∠DGC=∠GPO=∠FEM.
在△DCG和△FME中,
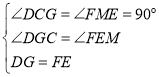 ,
,
∴△DCG≌△FME(AAS),
∴FM=DC=4.
∵MN⊥x轴,
∴四边形OMNC为矩形,
∴MN=OC=5,FN=MN-FM=1.
∴S=![]() BGFN=
BGFN=![]() (7-a).
(7-a).
∵点E在边OA上,点G在BC边上,且点G不与点C重合,
∴DE≤![]() ,a>0,
,a>0,
∴DG=![]() ,
,
∴0<a≤![]() .
.
∴S与a的函数表达式为S=![]() (7-a)(0<a≤
(7-a)(0<a≤![]() )
)


科目:初中数学 来源: 题型:
【题目】“低碳出行,绿色出行”,自行车逐渐成为人们喜爱的交通工具,宁波某运动商城的自行车销售量自2016年起逐年增加,据统计该商城2016年销售自行车768辆,2018年销售了1200辆.
(1)若该商城近四年的自行车销售量年平均增长率相同,请你预估:该商城2019年大概能卖出多少辆自行车?
(2)考虑到自行车需求的不断增加,本月该商场准备投入3万元再购进一批两种规格的自行车,已知![]() 型车的进价为500元/辆,售价为700元/辆,
型车的进价为500元/辆,售价为700元/辆,![]() 型车的进价为1000元/辆,售价为1300元/辆.根据销售经验,
型车的进价为1000元/辆,售价为1300元/辆.根据销售经验,![]() 型车不少于
型车不少于![]() 型车的2倍,但不超过
型车的2倍,但不超过![]() 型车的3.2倍,假设所进车辆全部售完,为使得利润最大,该商场该如何进货?
型车的3.2倍,假设所进车辆全部售完,为使得利润最大,该商场该如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
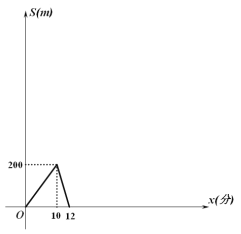
【题目】全民健身的今天,散步运动是大众喜欢的活动项目。家住同一小区的甲乙两人每天都在同一条如图1的阳光走道上来回散步.某天,甲乙两人同时从大道的A端以各自的速度匀速在大道上散步健身,步行一段时间后,甲接到消息有同事在出发地等他商量事务(甲收消息的时间忽略不计),于是甲按原速度返回,遇见乙后用原来的2倍速度跑步前往,此时乙仍按原计划继续散步运动,4分钟后甲结束了谈话,继续按原速度运动.图2是甲乙两人之间的距离S(m)与他们出发后的时间x(分)之间函数关系的部分图像,已知甲步行速度比乙快.
(1)由图像可知,甲的速度为___ ___m/分;乙的速度为_____m/分.
(2)若甲处理完事情继续按原速度散步,再次遇到乙后两人稍作放松后就各自回家,根据已有信息,就甲乙两人一起散步到第二次相遇的过程,请在图2中补全函数图像,并写出所补的图像中的S与x的函数关系式及x的取值范围.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
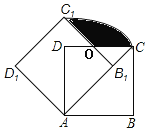
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则图中阴影部分的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() x+2与x轴交于点A,与y轴交于点C,抛物线y=
x+2与x轴交于点A,与y轴交于点C,抛物线y=![]() x2+bx+c经过A、C两点,与x轴的另一交点为点B.
x2+bx+c经过A、C两点,与x轴的另一交点为点B.

(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为S1, △BCE的面积为S2, 求![]() 的最大值;
的最大值;
②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
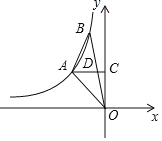
【题目】如图,A、B是反比例函数![]() 图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为______.
图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具商店销售学习用品,已知某品牌钢笔的进价是20元,销售过程发现,每月销量y支与销售单价x元(x为正整数)之间满足一次函数关系,且每支钢笔的售价不低于进价,也不高于35元,下表是y与x之间的对应数据:
销售单价x(元) | … | 22 | 24 | 30 | … |
月销量y(只) | … | 92 | 84 | 60 | … |
(1)求y与x的函数关系式并直接写出自变量x的取值范围.
(2)每支钢笔的售价定为多少元时,月销售利润恰为600元?
(3)每支钢笔的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
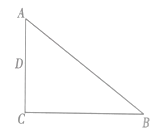
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点.
边的中点.
(1)尺规作图:作出以![]() 为直径的圆
为直径的圆![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .(保留作图痕迹,不写作法)
.(保留作图痕迹,不写作法)
(2)求证:![]() 是圆
是圆![]() 的切线.
的切线.
(3)当![]() 时,四边形
时,四边形![]() 是平行四边形,此时,四边形
是平行四边形,此时,四边形![]() 的形状为 .
的形状为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
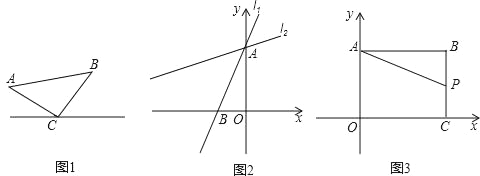
【题目】建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
实践操作:过点A作AD⊥l于点D,过点B作BE⊥l于点E,求证:△CAD≌△BCE.
模型应用:(1)如图2,在直角坐标系中,直线l1:y=![]() x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com