
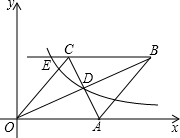
 如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=
如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y= (x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论:
(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,有下列四个结论: (x>0);②E点的坐标是(5,8);③sin∠COA=
(x>0);②E点的坐标是(5,8);③sin∠COA= ;④AC+OB=12
;④AC+OB=12 .其中正确的结论有
.其中正确的结论有 (x>0)的解析式,由反比例函数的解析式与直线BC的解析式联立即可求出E点坐标;由sin∠COA=
(x>0)的解析式,由反比例函数的解析式与直线BC的解析式联立即可求出E点坐标;由sin∠COA= 可求出∠COA的正弦值;根据A、C两点的坐标可求出AC的长,由OB•AC=160即可求出OB的长.
可求出∠COA的正弦值;根据A、C两点的坐标可求出AC的长,由OB•AC=160即可求出OB的长.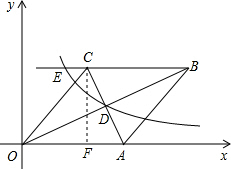 解:过点C作CF⊥x轴于点F,
解:过点C作CF⊥x轴于点F, OB•AC=
OB•AC= ×160=80,菱形OABC的边长为10,
×160=80,菱形OABC的边长为10, =
= =8,
=8, =
=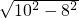 =6,
=6, ,
, ),即(8,4),
),即(8,4), (x>0)经过D点,
(x>0)经过D点, ,即k=32,
,即k=32,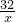 (x>0),故①错误;
(x>0),故①错误; ,解得x=4,y=8,
,解得x=4,y=8, =
= =
= ,故③正确;
,故③正确; =4
=4 ,
, =
= =8
=8 ,
, +8
+8 =12
=12 ,故④正确.
,故④正确.

科目:初中数学 来源: 题型:
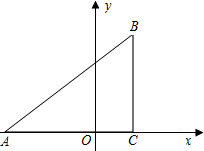 坐标分别为A(-3,0),C(1,0),tan∠BAC=
坐标分别为A(-3,0),C(1,0),tan∠BAC=| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•白下区一模)写出下列命题的已知、求证,并完成证明过程.
(2012•白下区一模)写出下列命题的已知、求证,并完成证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•浦东新区二模)已知:如图,在△ABC中,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在边AC上的点D处,点F在线段AE的延长线上,如果∠FCA=∠B=2∠ACB,AB=5,AC=9.
(2013•浦东新区二模)已知:如图,在△ABC中,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在边AC上的点D处,点F在线段AE的延长线上,如果∠FCA=∠B=2∠ACB,AB=5,AC=9.| BE | CF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com