
 中,
中,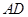 ∥
∥ ,
, ,
, .一个动点
.一个动点 从点
从点 出发,以每秒
出发,以每秒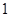 个单位长度的速度沿线段
个单位长度的速度沿线段 方向运动,过点
方向运动,过点 作
作 ,交折线段
,交折线段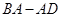 于点
于点 ,以
,以 为边向右作正方形
为边向右作正方形 ,点
,点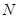 在射线
在射线 上,当
上,当 点到达
点到达 点时,运动结束.设点
点时,运动结束.设点 的运动时间为
的运动时间为 秒(
秒(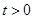 ).
). 的边
的边 恰好经过点
恰好经过点 时,求运动时间
时,求运动时间 的值;
的值; 与△
与△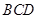 的重合部分面积为
的重合部分面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量 的取值范围;
的取值范围; 在线段
在线段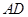 上运动时,线段
上运动时,线段 与对角线
与对角线 交于点
交于点 ,将△
,将△ 沿
沿 翻折,得到△
翻折,得到△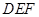 ,连接
,连接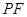 .是否存在这样的
.是否存在这样的 ,使△
,使△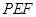 是等腰三角形?若存在,求出对应的
是等腰三角形?若存在,求出对应的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
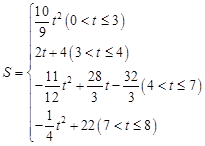
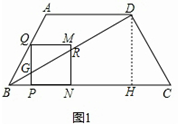
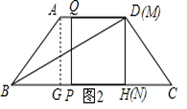
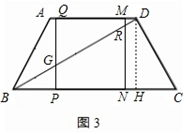
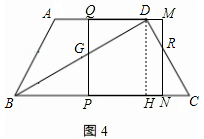
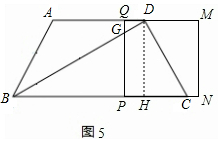
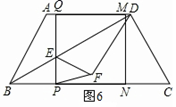
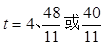 时,∆PEF是等腰三角形
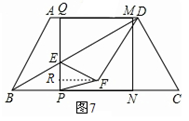
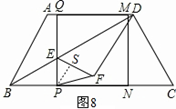
时,∆PEF是等腰三角形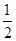 t,分为三种情况:EF=EP时可以求出t值,当FE=FP时,作FR⊥EP,垂足为R,可以求出t值,当PE=PF时,作PS⊥EF,垂足为S,可以求出t值.
t,分为三种情况:EF=EP时可以求出t值,当FE=FP时,作FR⊥EP,垂足为R,可以求出t值,当PE=PF时,作PS⊥EF,垂足为S,可以求出t值.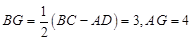 ,
,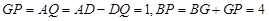 ,
,
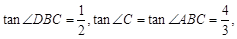
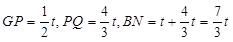 ,
,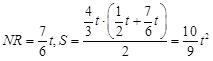
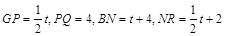
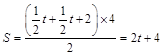
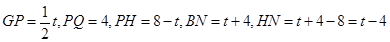
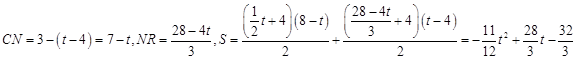
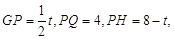
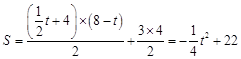
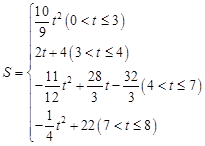
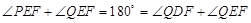 ,
,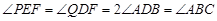
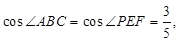
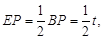 则
则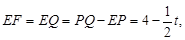
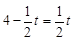

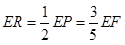
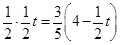
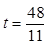
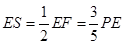
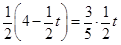
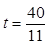
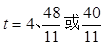 时,∆PEF是等腰三角形。
时,∆PEF是等腰三角形。

 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源:不详 题型:解答题
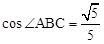 时,求AF及BE的长.
时,求AF及BE的长.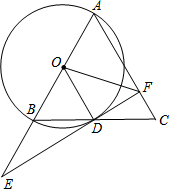
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
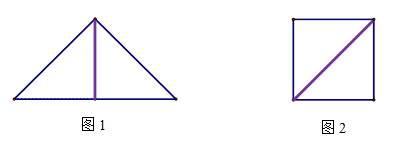
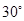 ,恰好可以拼成另一个含有30°角的直角三角形,那么在原来的两个三角形纸片中,较大的与较小的纸片的相似比为________,请画出拼接的示意图;
,恰好可以拼成另一个含有30°角的直角三角形,那么在原来的两个三角形纸片中,较大的与较小的纸片的相似比为________,请画出拼接的示意图;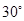 的直角三角形纸片拼成,请你画出两种不同拼法的示意图.在拼成这个矩形的三角形中,若每种拼法中最小的三角形的斜边长为
的直角三角形纸片拼成,请你画出两种不同拼法的示意图.在拼成这个矩形的三角形中,若每种拼法中最小的三角形的斜边长为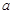 ,请直接写出每种拼法中最大三角形的斜边长.
,请直接写出每种拼法中最大三角形的斜边长.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.6.18 | B.0.382 | C.0.618 | D.3.82 |
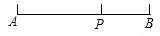
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.2:3 | B.2:5 | C.4:9 | D.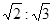 |
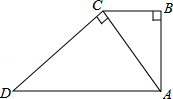
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
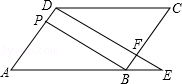
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
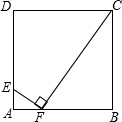
| A.1 | B.1.5 | C.2 | D.2.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com