
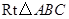 中,
中, ,
, ,
, 两点分别在
两点分别在 上,
上, ,
,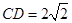 ,将
,将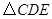 绕点
绕点 顺时针旋转,得到
顺时针旋转,得到 (如图4,点
(如图4,点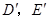 分别与
分别与 对应),点
对应),点 在
在 上,
上, 与
与 相交于点
相交于点 .
.
 的度数;
的度数; 是梯形;
是梯形; 的面积.
的面积. ,∴CE=CE′=4.
,∴CE=CE′=4.  ,CE′=4,∴cos∠ACE′=
,CE′=4,∴cos∠ACE′=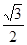 ,∴∠ACE′=30°.
,∴∠ACE′=30°. ,∴△D′CA∽△E′CB. ∴∠D′AC=∠B=45°,∴∠ACB=∠D′AC,∴AD′∥BC.
,∴△D′CA∽△E′CB. ∴∠D′AC=∠B=45°,∴∠ACB=∠D′AC,∴AD′∥BC. 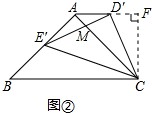
 ,∴S△ACF=3,
,∴S△ACF=3, ,∠FCD′=30°,∴D′F=
,∠FCD′=30°,∴D′F= ,
, .同理,SRt△AE′C=2
.同理,SRt△AE′C=2 ,SRt△D′E′C=4. ∵∠AME′=∠D′MC,∠E′AM=∠CD′M,
,SRt△D′E′C=4. ∵∠AME′=∠D′MC,∠E′AM=∠CD′M, .
.  S△CD′M.②∵S△EMC+S△AE′M=S△AE′C=2
S△CD′M.②∵S△EMC+S△AE′M=S△AE′C=2 ,
, ,
, ,∴S△AD′M=S△ACF-S△DCF-S△CD′M=3
,∴S△AD′M=S△ACF-S△DCF-S△CD′M=3 -5.∴△AD′M的面积是3
-5.∴△AD′M的面积是3 -5.
-5.

科目:初中数学 来源:不详 题型:填空题
 ≥3,且
≥3,且 为整数)
为整数)


查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 中,
中, 为
为 上一点,且
上一点,且 .
. 为等腰直角三角形,斜边
为等腰直角三角形,斜边 与
与 交于点
交于点 ,延长
,延长 与
与 的延长线交于点
的延长线交于点 ,连接
,连接 、
、 ,作
,作 ,垂足为
,垂足为 ,下列结论:①
,下列结论:① ≌
≌ ;②
;② 为等腰直角三角形;③
为等腰直角三角形;③ ;④
;④ ;⑤
;⑤ .其中正确的个数为( )
.其中正确的个数为( )
| A.2个 | B.3个 | C.4个 | D.5个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
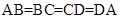 ,对角线AC与BD相交于点O.若不增加任何字母与辅助线,要使得四边形ABCD是正方形,则还需增加的一个条件是
,对角线AC与BD相交于点O.若不增加任何字母与辅助线,要使得四边形ABCD是正方形,则还需增加的一个条件是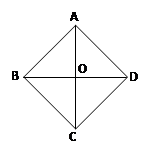
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.100° | B.110° | C.120° | D.130° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com