
先阅读,再回答问题:
如果x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,那么x1+x2,x1x2与系数a,b,c的关系是:x1+x2=- ,x1x2=
,x1x2= .例如:若x1,x2是方程2x2-x-1=0的两个根,则x1+x2=-
.例如:若x1,x2是方程2x2-x-1=0的两个根,则x1+x2=- =-
=- =
= ,x1x2=
,x1x2= =
= =-
=- .
.
若x1,x2是方程2x2+x-3=0的两个根,(1)求x1+x2,x1x2
(2)求 +
+ 的值.(3) 求(x1-x2)2.
的值.(3) 求(x1-x2)2.
(1) x1+x2=-0.5,x1x2=-1.5;(2)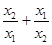 =
=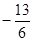 ;(3)(x1-x2)2=
;(3)(x1-x2)2=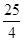 .
.
【解析】
试题分析:一元二次方程ax2+bx+c=0根与系数的关系:如果方程的两个实数根是x1,x2,那么x1+x2=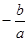 ,x1x2=
,x1x2=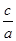 ,(1)由题, a=2,b=1,c=-3,x1+x2=-0.5,x1x2=-1.5;(2)通分后可以转化成两根和与乘积的式子,从而求解,
,(1)由题, a=2,b=1,c=-3,x1+x2=-0.5,x1x2=-1.5;(2)通分后可以转化成两根和与乘积的式子,从而求解,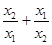 =
=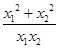 =
=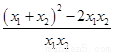 =
=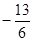 ;(3)去括号,利用完全平方公式a2±2ab+b2= (a±b)2)将式子转化成两根和与乘积的式子,(x1-x2)2=x12-2 x1x2+x22=(x1+x2)2
-4 x1x2=
;(3)去括号,利用完全平方公式a2±2ab+b2= (a±b)2)将式子转化成两根和与乘积的式子,(x1-x2)2=x12-2 x1x2+x22=(x1+x2)2
-4 x1x2=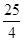 .
.
试题解析:(1)由题, a=2,b=1,c=-3,
x1+x2=-0.5,x1x2=-1.5;
(2)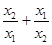
=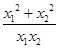
=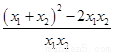
=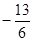 ;
;
(3)(x1-x2)2
=x12-2 x1x2+x22
=(x1+x2)2 -4 x1x2
=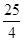 .
.
考点:一元二次方程根与系数关系.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:阅读理解
| b |
| a |
| c |
| a |
| b |
| a |
| -1 |
| 2 |
| 1 |
| 2 |
| c |
| a |
| -1 |
| 2 |
| 1 |
| 2 |
| x2 |
| x1 |
| x1 |
| x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| b |
| a |
| c |
| a |
| b |
| a |
| -1 |
| 2 |
| 1 |
| 2 |
| c |
| a |
| -1 |
| 2 |
| 1 |
| 2 |
| x2 |
| x1 |
| x1 |
| x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| b |
| a |
| c |
| a |
| a |
| b |
| -1 |
| 2 |
| 1 |
| 2 |
| c |
| a |
| -1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| x2 |
| x1 |
| x1 |
| x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| b |
| a |
| -1 |
| 2 |
| c |
| a |
| -1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| x2 |
| x1 |
| x1 |
| x2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 12+1 |
| 2 |
| 2 |
| 12+1 |
| 22+2 |
| 6 |
| 6 |
| 22+2 |
| 32+3 |
| 12 |
| 12 |
| 32+3 |
| a2+a |
| a2+a |
| a2+a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com