
【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=![]() ,OC=
,OC=![]() ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.

【答案】![]()
【解析】过O作OF⊥BC,过A作AM⊥OF,如图所示:
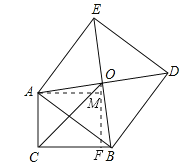
∵四边形ABDE为正方形,
∴∠AOB=90°,OA=OB,
∴∠AOM+∠BOF=90°,
又∠AMO=90°,
∴∠AOM+∠OAM=90°,
∴∠BOF=∠OAM,
在△AOM和△BOF中,
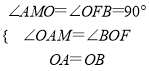 ,
,
∴△AOM≌△BOF(AAS),
∴AM=OF,OM=FB,
又∠ACB=∠AMF=∠CFM=90°,
∴四边形ACFM为矩形,
∴AM=CF,AC=MF=![]() ,
,
∴OF=CF,
∴△OCF为等腰直角三角形,
∵OC=![]() ,
,
∴根据勾股定理得:CF2+OF2=OC2,
解得:CF=OF=1,
∴FB=OM=OF-FM=1-![]() =
=![]()
则BC=CF+BF=1+![]() =
=![]() ;
;
故答案是: ![]() 。
。


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.

(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备随机选出七、八、九三个年级各1名学生担任学校国旗升旗手.现已知这三个年级每个年级分别选送一男、一女共6名学生作为备选人.
(1)请你利用树状图或表格列出所有可能的选法;
(2)求选出“一男两女”三名国旗升旗手的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市城区测得上一周PM2.5的日均值(单位mg/m3)如下:50,40,75,50,57,40,50.则这组数据的众数是( )
A. 40B. 50C. 57D. 75
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在线段
在线段![]() 的下方.
的下方.
(1)将图(1)中的直角三角板绕点![]() 按逆时针方向旋转,使
按逆时针方向旋转,使![]() 落在射线
落在射线![]() 上(如图(2)),则三角板旋转的角度为____度;
上(如图(2)),则三角板旋转的角度为____度;
(2)继续将图2中的直角三角板绕点![]() 按逆时针方向旋转,使
按逆时针方向旋转,使![]() 在
在![]() 的内部(如图3).试求
的内部(如图3).试求![]() 与
与![]() 度数的差;
度数的差;
(3)若图1中的直角三角板绕点![]() 按逆时针方向旋转一周,在此过程中:
按逆时针方向旋转一周,在此过程中:
①当直角边![]() 所在直线恰好垂直于
所在直线恰好垂直于![]() 时,
时, ![]() 的度数是________;
的度数是________;
②设直角三角板绕点![]() 按每秒
按每秒![]() 的速度旋转,当直角边
的速度旋转,当直角边![]() 所在直线恰好平分
所在直线恰好平分![]() 时,求三角板绕点
时,求三角板绕点![]() 旋转时间
旋转时间![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com