
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE 沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.
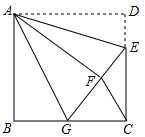
求证:(1)△ABG≌△AFG;
(2)求△FGC的面积.
【答案】(1)证明见解析;(2)3.6.
【解析】
试题分析:(1)利用翻折变换对应边关系得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;
(2)利用勾股定理得出GE2=CG2+CE2,进而求出BG即可;
(3)首先过C作CM⊥GF于M,由勾股定理以及由面积法得,CM=2.4,进而得出答案.
试题解析:(1)在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,
∵将△ADE沿AE对折至△AFE,
∴AD=AF,DE=EF,∠D=∠AFE=90°,
∴AB=AF,∠B=∠AFG=90°,
又∵AG=AG,
在Rt△ABG和Rt△AFG中,
∵![]()
∴△ABG≌△AFG(HL);
(2)过C作CM⊥GF于M,
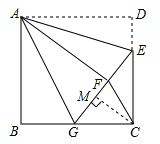
∵BG=GF=3,
∴CG=3,EC=6-2=4,
∴GE=![]() =5,
=5,
CM![]() GE=GC
GE=GC![]() EC,
EC,
∴CM×5=3×4,
∴CM=2.4,
∴S△FGC=![]() GF×CM=3.6.
GF×CM=3.6.


科目:初中数学 来源: 题型:
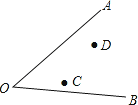
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.
(要求:用尺规作图,保留作图痕迹,写出作法,不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A. AC=BD,AB∥CD,AB=CDB. AD∥BC,∠A=∠C
C. AO=BO=CO=DO,AC⊥BDD. AO=CO,BO=DO,AB=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】除夕夜中央电视台举办的“2016年春节联欢晚会”受到广泛的关注.某组织就“2016年春节联欢晚会”节目的喜爱程度,在三峡广场进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D;根据调查结果绘制出如图所示的扇形统计图(未完成)和条形统计图(未完成),请结合图中所给信息解答下列问题
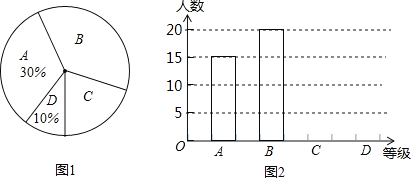
(1)本次被调查对象共有 人;被调查者“不太喜欢”有 人。
(2)将扇形统计图和条形统计图补充完整;
(3)在“非常喜欢”调查结果里有人为80后,其中3男2女,在这5人中,该组织打算随机选2位进行采访,请你用列表法或树状图法求出所选2位恰好都为男性的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽是同班同学,小明的家距学校2千米远,小丽的家距学校5千米远,设小明家距小丽家x千米远,则x的值应满足( )
A.x=3 B.x=7 C.x=3或x=7 D.3≤x≤7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com