
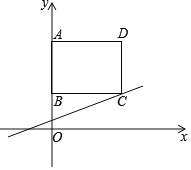
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、B、D的坐标分别为(0,5)、(0,2)、(4,5),直线l的解析式为y=kx+2﹣4k(k>0).
(1)当直线l经过原点O时,求一次函数的解析式;
(2)通过计算说明:不论k为何值,直线l总经过点C;
(3)在(1)的条件下,点M为直线l上的点,平面内是否存在x轴上方的点N,使以点O、A、M、N为顶点的四边形是菱形?若存在,请直接写出点M的坐标:若不存在,请说明理由.
【答案】(1)![]() ;(2)详见解析;(3)存在,满足条件的点M为
;(2)详见解析;(3)存在,满足条件的点M为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将原点坐标代入解析式可求出k的值,即可求解;
(2)由题意可得点C(4,2),当x=4时,y=4k+2﹣4k=2,则可得不论k为何值,直线l总经过点C;
(3)分OA为边,OA为对角线两种情况讨论,由菱形的性质可求解.
解:(1)∵直线l经过原点,
∴把点(0,0)代入y=kx+2﹣4k,
得:2﹣4k=0,
解得:![]() ,
,
∴一次函数的解析式为:![]() ;
;
(2)由题意可知,点C的坐标为(4,2),
当x=4时,y=4k+2﹣4k=2,
∴不论k为何值,直线l总经过点C;
(3)设点M(x,![]() x)
x)
①以OA为菱形的边,此时,OM=OA=5,
∴![]()
∴x=±2![]() ,
,
点M的坐标为![]() 或
或![]() ;
;
②以OA为菱形的一条对角线,
此时MN垂直平分OA,
则![]() x=
x=![]()
∴x=5
则M的坐标为![]() ;
;
综上所述:满足条件的点M为![]() 或
或![]() 或
或![]() .
.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
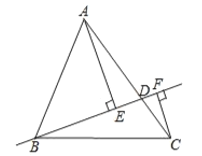
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上任意一点,分别过点
上任意一点,分别过点![]() 、
、![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() 、
、![]() ,
,![]() ,
,![]() ,则
,则![]() 的最大值是______________,最小值是______________.
的最大值是______________,最小值是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形组成的10×5网格,每个小正方形的顶点叫做格点,点A,B,C,D均在格点上,在网格中将点B按下列步骤移动第一步:点B绕点A逆时针旋转180°得到点B1;第二步:点B1绕点D逆时针旋转90°得到点B2;第三步:点B2绕点C逆时针旋转90°回到点B
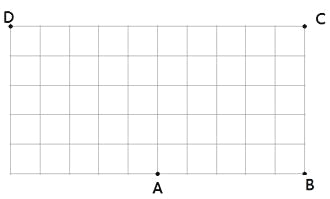
(1)请用圆规画出点B→B1→B2→B经过的路径;
(2)所画图形是_______图形;
(3)求所画图形的周长(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
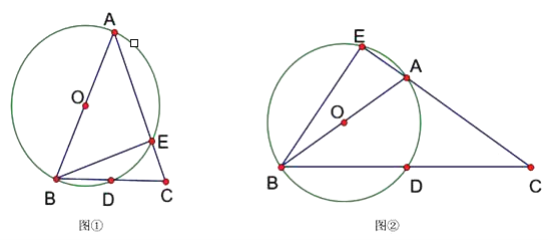
(1)当∠BAC为锐角时,如图①,求证:∠CBE=![]() ∠BAC;
∠BAC;
(2)当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组,对函数y=|x﹣1|+1的图象和性质进行了探究,探究过程如下:
(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | … |
其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
(3)根据画出的函数图象特征,仿照示例,完成下列表格中的函数变化规律:
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在直线x=1的右侧,函数图象呈上升状态 | 当x>1时,y随x的增大而增大 |
① | 在直线x=1的左侧,函数图象呈下降状态 |
|
示例2 | 函数图象经过点(﹣3,5) | 当x=﹣3时,y=5 |
② | 函数图象的最低点是(1,1) |
|
(4)当2<y≤4时,x的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两名射击选手中选出一名选手参加省级比赛,现对他们分别进行5次射击测试,成绩分别为(单位:环)
甲:5、6、7、9、8
乙:8、4、8、6、9
(1)分别计算这两组数据的平均数和方差;
(2)根据测试成绩,你认为选派哪一名选手参赛更好些?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传6月6日世界海洋日,某校八年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:

(1)本次调查一共随机抽取了个参赛学生的成绩;
(2)表1中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到90分以上(含90分)的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜店第一次用400元购进某种蔬菜,由于销售状况良好,该店又用700元第二次购进该品种蔬菜,所购数量是第一次购进数量的2倍,但进货价每千克少了0.5元.
(1)第一次所购该蔬菜的进货价是每千克多少元?
(2)蔬菜店在销售中,如果两次售价均相同,第一次购进的蔬菜有2% 的损耗,第二次购进的蔬菜有3% 的损耗,若该蔬菜店售完这些蔬菜获利不低于944元,则该蔬菜每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的一次函数,当x=1时,y=1;当x=-2时,y=-14.
(1)求这个一次函数的关系式;
(2)在如图所示的平面直角坐标系中作出函数的图像;
(3)由图像观察,当0≤x≤2时,函数y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com