
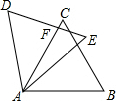
 如图,将边长为6的等边三角形ABC绕点A逆时针旋转30度后得到△AED,边AC与DE交于点F,则AF的长为3$\sqrt{3}$.
如图,将边长为6的等边三角形ABC绕点A逆时针旋转30度后得到△AED,边AC与DE交于点F,则AF的长为3$\sqrt{3}$. 分析 先根据旋转得出旋转角为30°,进而在Rt△ADF中,根据含30°角的直角三角形的性质得到DF长,最后根据勾股定理求得AF长即可.
解答 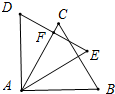 解:由旋转的性质可得,∠CAD=30°,∠D=∠C=60°,AD=AC=6,
解:由旋转的性质可得,∠CAD=30°,∠D=∠C=60°,AD=AC=6,
∴∠AFD=90°,
∴Rt△ADF中,DF=$\frac{1}{2}$AD=3,
∴AF=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 本题以旋转为背景,主要考查了等边三角形的性质以及勾股定理.在直角三角形中,30°角所对的直角边等于斜边的一半,此结论在解直角三角形的相关问题中常用来求边的长度和角的度数.


科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABD中,∠BDA=90°,AD=BD,点E在AD上,连接BE,将△BED绕点D顺时针旋转90°,得到△ACD,若∠BED=65°,则∠ACE的度数为( )
如图,在Rt△ABD中,∠BDA=90°,AD=BD,点E在AD上,连接BE,将△BED绕点D顺时针旋转90°,得到△ACD,若∠BED=65°,则∠ACE的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题:
小明一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,点E,点F在边AB,AC上,且EF∥BC,延长FE至点G,使GE=EF,连接CG交AB于点H.
如图,△ABC中,点E,点F在边AB,AC上,且EF∥BC,延长FE至点G,使GE=EF,连接CG交AB于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形纸片ABCD中,AD=5,AB=3,点E为BC上一点,沿着AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D.
如图,在矩形纸片ABCD中,AD=5,AB=3,点E为BC上一点,沿着AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com