
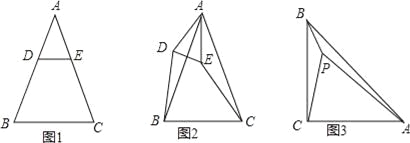
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
【答案】(1)=;(2)成立,证明见解析;(3)135°.
【解析】
试题(1)由DE∥BC,得到![]() ,结合AB=AC,得到DB=EC;
,结合AB=AC,得到DB=EC;
(2)由旋转得到的结论判断出△DAB≌△EAC,得到DB=CE;
(3)由旋转构造出△CPB≌△CEA,再用勾股定理计算出PE,然后用勾股定理逆定理判断出△PEA是直角三角形,在简单计算即可.
试题解析:(1)∵DE∥BC,
∴![]() ,
,
∵AB=AC,
∴DB=EC,
故答案为=,
(2)成立.
证明:由①易知AD=AE,
∴由旋转性质可知∠DAB=∠EAC,
又∵AD=AE,AB=AC
∴△DAB≌△EAC,
∴DB=CE,
(3)如图,
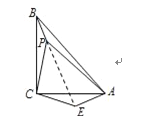
将△CPB绕点C旋转90°得△CEA,连接PE,
∴△CPB≌△CEA,
∴CE=CP=2,AE=BP=1,∠PCE=90°,
∴∠CEP=∠CPE=45°,
在Rt△PCE中,由勾股定理可得,PE=![]() ,
,
在△PEA中,PE2=(![]() )2=8,AE2=12=1,PA2=32=9,
)2=8,AE2=12=1,PA2=32=9,
∵PE2+AE2=AP2,
∴△PEA是直角三角形
∴∠PEA=90°,
∴∠CEA=135°,
又∵△CPB≌△CEA
∴∠BPC=∠CEA=135°.


科目:初中数学 来源: 题型:
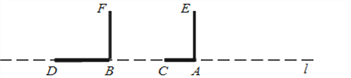
【题目】高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P的坐标为(m,n),则向量![]() 可以用点P的坐标表示为
可以用点P的坐标表示为![]() =(m,n);已知
=(m,n);已知![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),若x1x2+y1y2=0,则
=(x2,y2),若x1x2+y1y2=0,则![]() 与
与![]() 互相垂直.
互相垂直.
下面四组向量:①![]() =(3,﹣9),
=(3,﹣9),![]() =(1,﹣
=(1,﹣![]() );
);
②![]() =(2,π0),
=(2,π0),![]() =(2﹣1,﹣1);
=(2﹣1,﹣1);
③![]() =(cos30°,tan45°),
=(cos30°,tan45°),![]() =(sin30°,tan45°);
=(sin30°,tan45°);
④![]() =(
=(![]() +2,
+2,![]() ),
),![]() =(
=(![]() ﹣2,
﹣2,![]() ).
).
其中互相垂直的组有( )
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD>AB,点P是CD边上的任意一点(不含C,D两端点),过点P作PF∥BC,交对角线BD于点F.
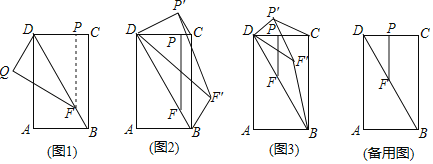
(1)如图1,将△PDF沿对角线BD翻折得到△QDF,QF交AD于点E.求证:△DEF是等腰三角形;
(2)如图2,将△PDF绕点D逆时针方向旋转得到△P'DF',连接P'C,F'B.设旋转角为α(0°<α<180°).
①若0°<α<∠BDC,即DF'在∠BDC的内部时,求证:△DP'C∽△DF'B.
②如图3,若点P是CD的中点,△DF'B能否为直角三角形?如果能,试求出此时tan∠DBF'的值,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
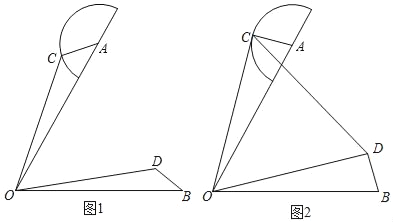
【题目】已知OA=OB=4,∠AOB=60°,半⊙A的半径为1,点C是半圆上任意一点,连结OC,把OC绕点O顺时针旋转6
0°到OD的位置,连结BD.
(1)如图1,求证:AC=BD.
(2)如图2,当OC与半圆相切于点C时,求CD的长.
(3)直接写出△AOC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
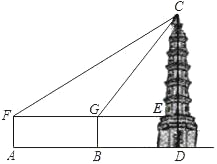
【题目】计算:在一次数学社团活动课上,同学们测量一座古塔CD的高度,他们首先在A处安置测量器,测得塔顶C的仰角∠CFE=30°,然后往塔的方向前进100米到达B处,此时测得塔顶C的仰角∠CGE=60°,已知测量器高1.5米,请你根据以上数据计算出古塔CD的高度.(保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴,并在所给坐标系中画出该函数的图象;
(3)该函数的图象经过怎样的平移得到y=x2的图象?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
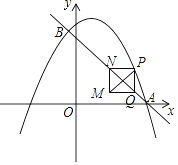
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com