
分析 先根据题中给出的例子找出规律,再进行计算即可.
解答 解:∵$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$…,
∴$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$
=1-$\frac{1}{2015}$
=$\frac{2014}{2015}$.
点评 本题考查的是有理数的混合运算,根据题意找出规律是解答此题的关键.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:填空题
 在四边形ABCD中,∠C=90°,∠ABC=∠ADB,BD平分∠ABC,AD:AB=$\sqrt{13}$:6,DC=1,则DB=$\frac{\sqrt{13}}{2}$.
在四边形ABCD中,∠C=90°,∠ABC=∠ADB,BD平分∠ABC,AD:AB=$\sqrt{13}$:6,DC=1,则DB=$\frac{\sqrt{13}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
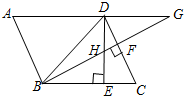 如图,平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE,②△BHE∽△BCF,③AB=BH,④△BHD∽△BDG,其中正确的结论是( )
如图,平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE,②△BHE∽△BCF,③AB=BH,④△BHD∽△BDG,其中正确的结论是( )| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
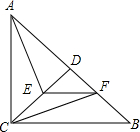 等腰直角△ABC中,∠ACB=90°,AC=BC,D为AB中点,E为CD上一点,EF∥BC,连AE,CF,若AC=AF.
等腰直角△ABC中,∠ACB=90°,AC=BC,D为AB中点,E为CD上一点,EF∥BC,连AE,CF,若AC=AF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com