
| 类别 | 甲种客车 | 乙种客车 |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 1000 | 800 |
分析 (1)根据题意可列出y与x的等式关系,再化简整理得出x,y的表达式;
(2)利用租车总费用不超过6500元,得出不等式求出x的取值范围,即可得出租车方案.
解答 解:(1)设租用甲种客车x辆,
y=1000x+(7-x)×800=200x+5600;
(2)因为租车总费用不超过6500元,
可得:200x+5600≤6500,
解得:x≤4.5,
因为取整数,所以x=4,3,2,1,
共有4种租车方案;
甲种客车4辆,乙种客车3辆,总载客量=4×45+3×30=270;
甲种客车3辆,乙种客车4辆,总载客量=3×45+4×30=255;
甲种客车2辆,乙种客车5辆,总载客量=2×45+5×30=240;
甲种客车1辆,乙种客车6辆,总载客量=1×45+6×30=225;
故甲种客车4辆,乙种客车3辆总载客量最大.
点评 此题主要考查了一次函数的应用以及不等式组的解法和一次函数的增减性,根据已知得出y与x的函数关系式是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
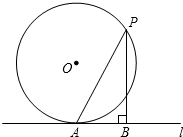 如图,直线l与半径为3的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA,设PA=m,PB=n,则m-n的最大值是( )
如图,直线l与半径为3的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA,设PA=m,PB=n,则m-n的最大值是( )| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
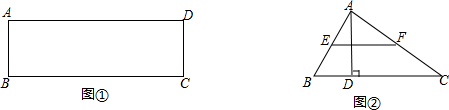
 如图,Rt△ABC中,∠C=90°,AC=8,BC=6,点是AB上的一个动点(不与A,B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况( )
如图,Rt△ABC中,∠C=90°,AC=8,BC=6,点是AB上的一个动点(不与A,B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况( )| A. | 先增大后减少 | B. | 先减少后增大 | C. | 逐渐增大 | D. | 逐渐减少 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
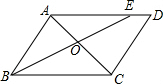 如图,在平行四边形ABCD中,点E在AD上,已知AE=3ED=6cm,OC=4cm,则AC的长为( )
如图,在平行四边形ABCD中,点E在AD上,已知AE=3ED=6cm,OC=4cm,则AC的长为( )| A. | 9cm | B. | 7cm | C. | 6cm | D. | 8cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
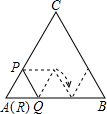 如图,正△ABC的边长为9cm,边长为3cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为6πcm.(结果保留π)
如图,正△ABC的边长为9cm,边长为3cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为6πcm.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
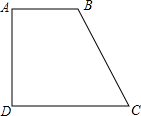 如图,在四边形ABCD中,AB∥CD,AB=12,BC=17,CD=20,AD=15.
如图,在四边形ABCD中,AB∥CD,AB=12,BC=17,CD=20,AD=15.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com