
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F . 过点E作EG∥BC , 交AB于G , 则图中相似三角形有( ) 
A.4对
B.5对
C.6对
D.7对
【答案】B
【解析】解答:图中相似三角形有△ABC∽△CDA , △AGE∽△ABC , △AFE∽△CBE , △BGE∽△BAF , △AGE∽△CDA共5对, 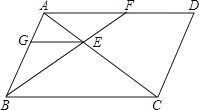
理由是:∵四边形ABCD是平行四边形,
∴AD∥BC , AB∥CD , AD=BC , AB=CD , ∠D=∠ABC ,
∴△ABC≌△CDA , 即△ABC∽△CDA ,
∵GE∥BC ,
∴△AGE∽△ABC∽△CDA ,
∵GE∥BC , AD∥BC ,
∴GE∥AD ,
∴△BGE∽△BAF ,
∵AD∥BC ,
∴△AFE∽△CBE .
故选B .
分析:根据平行四边形的性质得出AD∥BC , AB∥CD , AD=BC , AB=CD , ∠D=∠ABC , 推出△ABC≌△CDA , 即可推出△ABC∽△CDA , 根据相似三角形的判定定理:平行于三角形一边的直线截其它两边或其它两边的延长线,所截的三角形与原三角形相似即可推出其它各对三角形相似.
【考点精析】掌握相似三角形的判定是解答本题的根本,需要知道相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AD>AB. 
(1)作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的三边长分别为6cm , 7.5cm , 9cm , △DEF的一边长为4cm , 当△DEF的另两边长是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm
B.4 cm,5 cm
C.5 cm,6 cm
D.6 cm,7 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是( ) 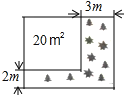
A.7m
B.8m
C.9m
D.10m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为°. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com