
(2013年四川南充8分)如图,二次函数y=x2+bx-3b+3的图象与x轴交于A、B两点(点A在点B的左边),交y轴于点C,且经过点(b-2,2b2-5b-1).

(1)求这条抛物线的解析式;
(2)⊙M过A、B、C三点,交y轴于另一点D,求点M的坐标;
(3)连接AM、DM,将∠AMD绕点M顺时针旋转,两边MA、MD与x轴、y轴分别交于点E、F,若△DMF为等腰三角形,求点E的坐标.
解:(1)把点(b-2,2b2-5b-1)代入y=x2+bx-3b+3,得
2b2-5b-1=(b-2)2+b(b-2)-3b+3, 解得b=2。
∴抛物线的解析式为y=x2+2x-3。
(2)由x2+2x-3=0,得x=-3或x=1。∴A(-3,0)、B(1,0)。
由x=0得y=-3,∴(0,-3)。
∵抛物线的对称轴是直线x=-1,圆心M在直线x=-1上,
∴设M(-1,n),作MG⊥x轴于G,MH⊥y轴于H,连接MC、MB。
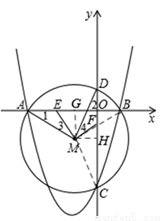
∴MH=1,BG=2。
∵MB=MC,∴BG2+MG2=MH2+CH2,
即4+n2=1+(3+n)2,解得n=-1。∴点M(-1,-1)。
(3)如图,由M(-1,-1),得MG=MH。
∵MA=MD,∴Rt△AMG≌RtDMH。∴∠1=∠2。
由旋转可知∠3=∠4, ∴△AME≌△DMF。
若△DMF为等腰三角形,则△AME为等腰三角形。
设E(x,0),△AME为等腰三角形,分三种情况:
①AE=AM=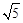 ,则x=
,则x=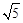 -3,∴E(
-3,∴E(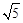 -3,0)。
-3,0)。
②∵M在AB的垂直平分线上,∴MA=ME=MB,∴E(1,0)。
③点E在AM的垂直平分线上,则AE=ME,
AE=x+3,ME2=MG2+EG2=1+(-1-x)2,
∴(x+3)2=1+(-1-x)2,解得x= ,∴E(
,∴E( ,0)。
,0)。
∴所求点E的坐标为(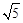 -3,0),(1,0),(
-3,0),(1,0),( ,0)。
,0)。
【解析】(1)将点(b-2,2b2-5b-1)代入抛物线解析式,求出未知数,从而得到抛物线的解析式。
(2)利用垂径定理及勾股定理,求出点M的坐标。
(3)首先,证明△AME≌△DMF,从而将“△DMF为等腰三角形”的问题,转化为“△AME为等腰三角形”的问题;其次,△AME为等腰三角形,可能有三种情形,需要分类讨论,逐一解析计算。
考点:二次函数综合题,旋转问题,曲线上点的坐标与方程的关系,垂径定理,勾股定理,全等三角形的判定和性质,等腰三角形的性质,分类思想的应用。


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源:2013年初中毕业升学考试(四川南充卷)数学(解析版) 题型:解答题
(2013年四川南充8分)如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10千米处是村庄N(参考数据:sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75).

(1)求M,N两村之间的距离;
(2)要在公路AB旁修建一个土特产收购站P,使得M,N两村到P站的距离之和最短,求这个最短距离。
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川南充卷)数学(解析版) 题型:解答题
(2013年四川南充8分)关于x的一元二次方程为(m-1)x2-2mx+m+1=0
(1)求出方程的根;
(2)m为何整数时,此方程的两个根都为正整数?
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川南充卷)数学(解析版) 题型:解答题
(2013年四川南充8分)如图,等腰梯形ABCD中,AD∥BC,AD=3,BC=7,∠B=60°,P为BC边上一点(不与B,C重合),过点P作∠APE=∠B,PE交CD 于E.

(1)求证:△APB∽△PEC;
(2)若CE=3,求BP的长.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川南充卷)数学(解析版) 题型:选择题
(2013年四川南充3分)计算-2+3的结果是【 】
A.-5 B. 1 C.-1 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com