
分析 直接利用已知分别得出∠AOB以及∠AOP和∠BOP的角平分线,进而利用角平分线的定义分析得出答案.
解答 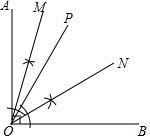 解:(1)如图所示:∠AOB=90°;
解:(1)如图所示:∠AOB=90°;
(2)如图所示:OP即为所求;
(3)如图所示:射线OM,ON即为所求;
(4)∠MON=45°,
理由:∵OM平分∠AOP,
∴∠AOM=∠MOP,
∴∠MOP=$\frac{1}{2}$∠AOP,
∵ON平分∠POB,
∴∠PON=∠BON,
∴∠PON=$\frac{1}{2}$∠POB,
∴∠MON=∠MOP+∠PON=$\frac{1}{2}$∠AOP+$\frac{1}{2}$∠POB=$\frac{1}{2}$∠AOB=45°.
故答案为:45°.
点评 此题主要考查了基本作图以及角平分线的作法与定义,正确把握角平分线的定义是解题关键.


科目:初中数学 来源: 题型:选择题
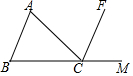 如图,点C在射线BM上,CF是∠ACM的平分线,且CF∥AB,∠ACB=50°,则∠B的度数为( )
如图,点C在射线BM上,CF是∠ACM的平分线,且CF∥AB,∠ACB=50°,则∠B的度数为( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | $\frac{\sqrt{12}-\sqrt{10}}{2}$=$\sqrt{6}-\sqrt{5}$ | D. | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当x=4时,式子有最大值-17 | B. | 当x=4时,式子有最小值-17 | ||
| C. | 当x=2时,式子有最大值-13 | D. | 当x=2时,式子有最小值-13 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
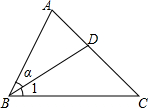 老师提出了以下问题:请用恰当的方法表示图中给出的所有角(小于平角的角),某组同学在本组展示区的答案是:∠1、∠α、∠BAD、∠C、∠D.
老师提出了以下问题:请用恰当的方法表示图中给出的所有角(小于平角的角),某组同学在本组展示区的答案是:∠1、∠α、∠BAD、∠C、∠D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
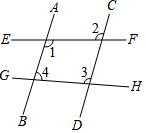 如图,下列判断中正确的是( )
如图,下列判断中正确的是( )| A. | 如果EF∥GH,那么∠4+∠3=180° | B. | 如果AB∥CD,那么∠1+∠4=180° | ||
| C. | 如果AB∥CD,那么∠1=∠2 | D. | 如果AB∥CD,那么∠2=∠3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com