
(1)证明:∵AC为半圆的直径,
∴∠ABC=∠CBO=90°,∠AEC=90°;
∵△ABC为等腰三角形,
∴BA=BC;
∵∠AEC=90°,点C、E、O在同一直线上,
∴∠AEO=90°,
∴∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2;
在△ABF与△CBO中,
∵
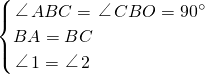
,
∴△ABF≌△CBO,
∴BF=BO.
(2)解:∵点B(t,0),
∴BF=BO=-1,即点F的坐标(t,-t);
y=a(x
2-2x)=a(x-1)
2-a,即原抛物线的顶点为(1,-a);
由题意知,抛物线H的解析式可记为y=a(x+1)
2-a;
∵抛物线H过点F(t,-t),
∴-t=a(t+1)
2-a,at
2+2at+a-a=-t
即:a=

=-

(-1<t<0).
(3)解:∵O、M是抛物线y=a(x
2-2x)与x轴的交点,
∴O(0,0)、M(2,0);
由题意知:A(-2,0)、OA=2;
∵AE过△ACO的内心I,
∴∠1=∠4;
∵∠AEC=∠AEO=90°,AE=AE
∴△ACE≌△AOE,
∴AC=AO,且AC与AO关于直线AE对称;
在Rt△ABC中,AC=2,∠ACB=45°,
∴AB=

,
∴BO=2-

,t=

-2;
此时抛物线H的解析式为y=-

(x
2+2x),即:y=-

x
2-

x.
(4)解:由(3)可知,直线AC与AO关于直线AE对称,所以只要直线AC与抛物线H有交点,那么就存在满足题意的点P;
设直线AC的解析式为y=kx+b,代入点A(-2,0)、C(

-2,

),得:

,
解得
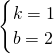
故直线AC:y=x+2;
联立直线AC和抛物线的解析式,有:

,
解得
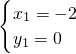
,

故所求点P的坐标为P
1(-2,0)、P
2(-

,2-

),即在抛物线H上存在点P
1和P
2,其关于直线AF的对称点在x轴上.
分析:(1)通过观察图形,若证线段相等,可以证明它们所在的三角形全等,即证△OBC、△FBA全等即可;这两个三角形中,∠FAB、∠BCO对应的是同一段弧,所以这一对角相等,而∠CBO、∠ABF都是直角,且AB、BC是等腰三角形的腰,不难判断这两个三角形全等,则题目可证.
(2)由(1)的结论可以得出点F的坐标,而平移后的抛物线H可由“左加右减、上加下减”的平移规律得出,将点F的坐标代入抛物线H的解析式中求解即可.
(3)在(2)中,已经求出了用t表示出来的抛物线H的解析式,所以此题的关键是求出t的值;点I是△AOC的内心,所以直线AE是∠CAO的角平分线,即直线AC、AO关于直线AE对称,而AE⊥OC(圆周角定理),那么显然△AOC是等腰三角形,且AO=AC;抛物线左移2个单位后,O、A以及M、O重合,所以OA=OM=2,由此不难看出AO=AC=2;而△ABC是等腰直角三角形,由此可以求出AB的长,由OB=OA-AB即可得出t的值,由此得解.
(4)在(3)题中已经明确了直线AC、AO关于直线AE对称,且AO正好位于x轴上,所以直线AC与抛物线的交点都符合点P的要求.
点评:考查了二次函数和圆的综合题,涉及了二次函数解析式的确定、圆周角定理、三角形的内心、全等三角形的判定和性质以及轴对称图形的性质等重要知识点;后面三题环环相扣,紧扣图形是解题的主要思路.

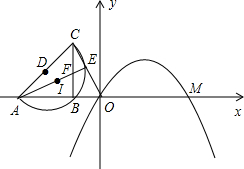 如图,在直角坐标系中,已知点A、B在x轴上,且B(t,0)(-1<t<0),等腰△ABC的顶点B在以AC为直径的半圆D上,点E是直线OC与半圆D除点C以外的另一个交点,连接AE与BC相交于点F.又已知抛物线y=a(x2-2x)向左平移2个单位长度后点O恰与点A重合、点M恰与原点O重合,并把平移后所得抛物线记为H.
如图,在直角坐标系中,已知点A、B在x轴上,且B(t,0)(-1<t<0),等腰△ABC的顶点B在以AC为直径的半圆D上,点E是直线OC与半圆D除点C以外的另一个交点,连接AE与BC相交于点F.又已知抛物线y=a(x2-2x)向左平移2个单位长度后点O恰与点A重合、点M恰与原点O重合,并把平移后所得抛物线记为H. (1)证明:∵AC为半圆的直径,
(1)证明:∵AC为半圆的直径,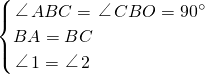 ,
, =-
=- (-1<t<0).
(-1<t<0). ,
, ,t=
,t= -2;
-2; (x2+2x),即:y=-
(x2+2x),即:y=- x2-
x2- x.
x. -2,
-2, ),得:
),得: ,
,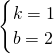
 ,
,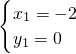 ,
,
 ,2-
,2- ),即在抛物线H上存在点P1和P2,其关于直线AF的对称点在x轴上.
),即在抛物线H上存在点P1和P2,其关于直线AF的对称点在x轴上.

 备战中考寒假系列答案
备战中考寒假系列答案
 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: