
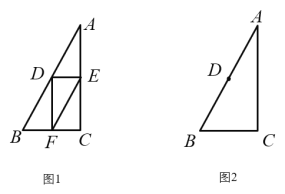
【题目】在![]() 中,∠C=90°,AC>BC,D是AB的中点.E为直线上一动点,连接DE,过点D作DF⊥DE,交直线BC于点F,连接EF.
中,∠C=90°,AC>BC,D是AB的中点.E为直线上一动点,连接DE,过点D作DF⊥DE,交直线BC于点F,连接EF.
(1)如图1,当E是线段AC的中点时,设![]() ,求EF的长(用含
,求EF的长(用含![]() 的式子表示);
的式子表示);
(2)当点E在线段CA的延长线上时,依题意补全图2,用等式表示线段AE,EF,BF之间的数量关系,并证明.
【答案】(1)![]() ;(2)图见解析,
;(2)图见解析,![]() ,证明见解析.
,证明见解析.
【解析】
(1)先根据中位线定理和线段中点定义可得![]() ,
,![]() ,
,![]() ,再根据平行四边形的性质、矩形的判定与性质可得
,再根据平行四边形的性质、矩形的判定与性质可得![]() ,从而可得
,从而可得![]() ,然后利用勾股定理即可得;
,然后利用勾股定理即可得;
(2)如图(见解析),先根据平行线的性质可得![]() ,
,![]() ,再根据三角形全等的判定定理与性质可得
,再根据三角形全等的判定定理与性质可得![]() ,
,![]() ,然后根据垂直平分线的判定与性质可得
,然后根据垂直平分线的判定与性质可得![]() ,最后在
,最后在![]() 中,利用勾股定理、等量代换即可得证.
中,利用勾股定理、等量代换即可得证.
(1)∵D是AB的中点,E是线段AC的中点
∴DE为![]() 的中位线,且
的中位线,且![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴四边形DECF为矩形
∴![]()
![]()
∴![]()
则在![]() 中,
中,![]() ;
;
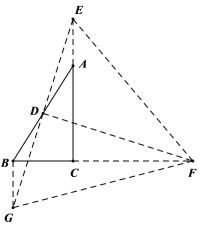
(2)过点B作AC的平行线交ED的延长线于点G,连接FG
∵![]()
∴![]() ,
,![]()
∵D是AB的中点
∴![]()
在![]() 和
和![]() 中,
中,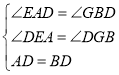
∴![]()
∴![]() ,
,![]()
又∵![]()
∴DF是线段EG的垂直平分线
∴![]()
∵![]() ,
,![]()
∴![]()
在![]() 中,由勾股定理得:
中,由勾股定理得:![]()
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:![]() )是反比例函数关系.当
)是反比例函数关系.当![]() 时,
时,![]() .
.
(1)写出I关于R的函数解析式;
(2)完成下表,并在给定的平面直角坐标系中画出这个函数的图象;
| … | … | ||||||||
| … | … |
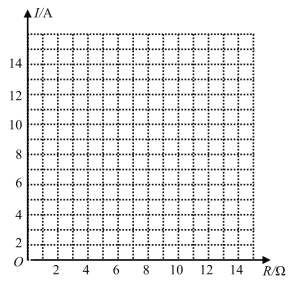
(3)如果以此蓄电池为电源的用电器的限制电流不能超过![]() .那么用电器可变电阻应控制在什么范围内?
.那么用电器可变电阻应控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
(1)求抛物线的表达式及顶点D的坐标;
(2)联结AD、AC、CD,求∠DAC的正切值;
(3)如果点P是原抛物线上的一点,且∠PAB=∠DAC,将原抛物线向右平移m个单位(m>0),使平移后新抛物线经过点P,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象由函数
的图象由函数![]() 的图象平移得到,且经过点(1,2).
的图象平移得到,且经过点(1,2).
(1)求这个一次函数的解析式;
(2)当![]() 时,对于
时,对于![]() 的每一个值,函数
的每一个值,函数![]() 的值大于一次函数
的值大于一次函数![]() 的值,直接写出
的值,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() ,
,![]() 两地相距
两地相距![]() .甲、乙两人都由
.甲、乙两人都由![]() 地去
地去![]() 地,甲骑自行车,平均速度为
地,甲骑自行车,平均速度为![]() ;乙乘汽车,平均速度为
;乙乘汽车,平均速度为![]() ,且比甲晚
,且比甲晚![]() 出发.设甲的骑行时间为
出发.设甲的骑行时间为![]() .
.
(1)根据题意,填写下表:
时间 与 | 0.5 | 1.8 | ______ |
甲与 | 5 | ______ | 20 |
乙与 | 0 | 12 | ______ |
(2)设甲,乙两人与![]() 地的距离为
地的距离为![]() 和
和![]() ,写出
,写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)设甲,乙两人之间的距离为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com